时间:2018-10-01 01:33:22
1、简答题 一个质点从静止开始做匀加速直线运动.已知它在?第4s内?的位移是14m.求:
(1)质点运动的加速度;
(2)它前进72m所用的时间.
参考答案:(1)因为质点从静止开始运动,故令质点运动的加速度为a,第4s内的位移x4=14m
则根据x=12at2得:
第4s内的位移为x4=(12a×42-12a×32)m? 得:
a=2×1442-32m/s2=4m/s2
(2)因为质点做初速度为0的匀加速直线运动,已知a=4m/s2,x=72m,求时间t
据x=12at2得
t=
本题解析:
本题难度:一般
2、选择题 做匀减速直线运动的质点,它的位移随时间变化的规律是s=24t-1.5t2(m),当质点的速度为零,则t为多少(?)
A.1.5s
B.8s
C.16s
D.24s
参考答案:B
本题解析:根据公式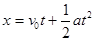 可得,该物体的初速度为
可得,该物体的初速度为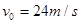 ,加速度为
,加速度为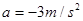 ,所以根据公式
,所以根据公式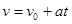 可得,当
可得,当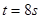 时,速度为零,B正确,
时,速度为零,B正确,
点评:此类型的题目是一种很常规的题,较易,关键是对公式的理解
本题难度:简单
3、简答题 汽车由静止开始做匀加速运动,经过4s速度增加到8m/s,接着做匀速运动,10s后改做匀减速直线运动,再经过8s恰好停止运动,求:
(1)求汽车在加速阶段的加速度和减速阶段的加速度
(2)汽车的总位移
(3)若保持车匀加速运动的加速度不变,匀减速运动的加速度也不变,完成上述位移又恰好停止的最短时间是多少?
参考答案:(1)汽车加速阶段的加速度a1=△v△t=8-04m/s2=2m/s2,
汽车减速阶段的加速度a2=△v△t=0-88m/s2=-1m/s2.
(2)汽车在加速阶段的位移x1=v2t1=82×4m=16m,
匀速运动的位移x2=vt=8×10m=80m
减速阶段的位移x3=v2×t3=32m
所以总位移x=x1+x2+x3=128m.
(3)当汽车匀加速运动后立即做匀减速运动,通过该段位移所需的时间最短.
设最大速度为vm,则
a1=vmt1,a2=-vmt2
x=vm2(t1+t2)
联立解得t1+t2=8
本题解析:
本题难度:一般
4、选择题 一质点做直线运动,其v-t图象如图所示.则( )
A.0.5s未和3.5s未速度方向相反
B.3.5s未和4.5s未速度方向相反
C.0.5s未和4.5s未加速度方向相反
D.0.5s未比4.5s未的加速度大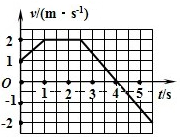
参考答案:
A、0.5s末和3.5s末的速度均为正值,速度方向均沿正方向,方向相同.故A错误.
B、3.5s末的速度为正值,沿正方向,而4.5s末的速度为负值,沿负方向,两个时刻速度方向相反.故B正确.
C、根据速度图象的斜率等于加速度可知,0.5s末加速度沿正方向,而4.5s末加速度沿负方向,加速度方向相反.故C正确.
D、由数学知识得知0.5s末与4.5s末的加速度大小相等.故D错误.
故选BC
本题解析:
本题难度:简单
5、计算题 如图所示,在一次警车A追击劫匪车B时,两车同时由静止向同一方向加速行驶,经过30 s追上。两车各自的加速度为aA=15 m/s2,aB=10 m/s2,各车最高时速分别为vA=45 m/s,vB=40 m/s,问追上时各行驶多少路程?原来相距多远?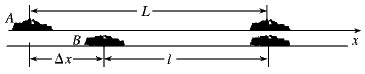
参考答案:解:以A为坐标原点,Ax为正向,令L为警车追上匪劫车所走过的全程,l为匪劫车走过的全程
则两车原来的间距为ΔL=L-l
设两车加速用的时间分别为tA1、tB1,以最大速度匀速运动的时间分别为tA2、tB2,则
vA=aAtA1,tA1=3 s,tA2=30 s-3 s=27 s
同理tB1=4 s,tB2=30 s-4 s=26 s
警车在0~tA1时段内做匀加速运动,L1=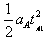 ,在3~30 s时段内做匀速运动;L2=vA(t-tA1),追上匪劫车的全部行程为L=L1+L2=
,在3~30 s时段内做匀速运动;L2=vA(t-tA1),追上匪劫车的全部行程为L=L1+L2=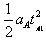 +vA(t-tA1)=
+vA(t-tA1)=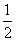 ×15×32 m+45×(30-3) m=1282.5 m
×15×32 m+45×(30-3) m=1282.5 m
同理匪车被追上时的全部行程为l=l1+l2=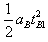 +vB(t-tB1)=1120 m
+vB(t-tB1)=1120 m
两车原来相距ΔL=L-l=1282.5 m-1120 m=162.5 m
本题解析:
本题难度:困难