时间:2018-03-18 10:00:54
1、选择题 如图所示，两根足够长的平行光滑金属导轨与水平方向成θ角放置，下端接有电阻R，一根质量为m的导体棒垂直放置在导轨上，与导轨保持良好接触，匀强磁场垂直导轨平面向上，导体棒在外力作用下向上匀速运动。不计导体棒和导轨的电阻，则下列说法正确的是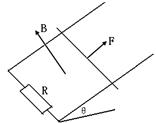
A．拉力做的功等于棒的机械能的增量
B．合力对棒做的功等于棒动能的增量
C．拉力与棒受到的磁场力的合力为零
D．拉力对棒做的功与棒克服重力做功之差等于回路中产生的电能
参考答案：BD
本题解析：本题考查的是电磁感应定律与力学的综合应用问题，导体棒在外力作用下向上匀速运动，则棒受力平衡，拉力F等于重力沿斜面向下的分力加上安培力；C错误；不计导体棒和导轨的电阻，拉力的功与安培力的功之和等于棒的机械能的增量，A错误，合力对棒做的功等于棒动能的增量；B正确；拉力对棒做的功与棒克服重力做功之差等于回路中产生的电能，D正确；
本题难度：简单
2、计算题 如图，直线MN 上方有平行于纸面且与MN成45°的有界匀强电场，电场强度大小未知；MN下方为方向垂直于纸面向里的有界匀强磁场，磁感应强度大小为B．今从MN 上的O点向磁场中射入一个速度大小为v、方向与MN成45°角的带正电粒子，该粒子在磁场中运动时的轨道半径为R ．该粒子从O点出发记为第一次经过直线MN ，第五次经过直线MN时恰好又通过O点．不计粒子的重力．
（1）画出粒子在磁场和电场中运动轨迹的草图；
（2）求出电场强度E的大小；
（3）求该粒子再次从O点进入磁场后，运动轨道的半径r；
（4）求该粒子从O点出发到再次回到O点所需的时间t ；
参考答案：（1）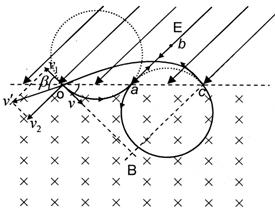
（2）
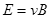（3）
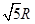（4）
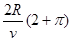
本题解析：（1）粒子的运动轨迹如图。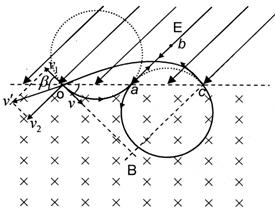
（2）由几何关系得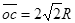
，粒子从c到o做类平抛运动，且在垂直、平行电场方向上的位移相等，都为
?
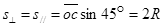类平抛运动时间为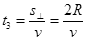
?
又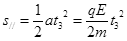
又?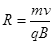
联立得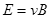
（3）粒子在电场中的加速度为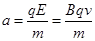
，
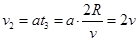?，v1=v.
粒子第五次过MN进入磁场后的速度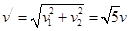 
则第五次过MN进入磁场后的圆弧半径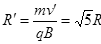
（4）粒子在磁场中运动的总时间为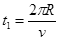
粒子做直线运动所需时间为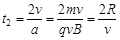
联立得粒子从出发到第五次到达O点所需时间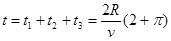
本题难度：一般
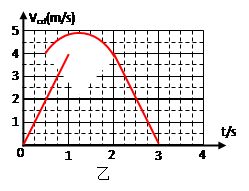
3、计算题 两根相距L=0.5m的足够长的金属导轨如图甲所示放置，他们各有一边在同一水平面上，另一边垂直于水平面。金属细杆ab、cd的质量均为m=0.05kg，电阻均为R=1.0Ω，它们与导轨垂直接触形成闭合回路，杆与导轨之间的动摩擦因数μ=0.5，导轨电阻不计。整个装置处于磁感应强度大小B=1.0T、方向竖直向上的匀强磁场中。当ab杆在平行于水平导轨的拉力F作用下沿导轨向右运动时，从某一时刻开始释放cd杆，并且开始计时，cd杆运动速度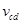
随时间变化的图像如图乙所示（在0～1s和2~3s内，对应图线为直线。g=10m/s2）。求：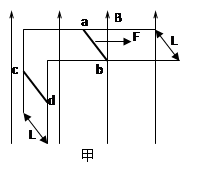
（1）在0~1s时间内，回路中感应电流I1的大小；
（2）在0～3s时间内，ab杆在水平导轨上运动的最大速度Vm；
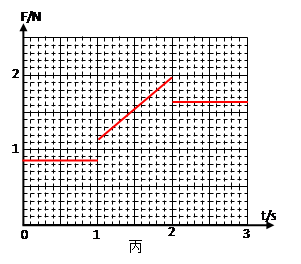
（3）已知1～2s内，ab杆做匀加速直线运动，写出1～2s内拉力F随时间t变化的关系式，并在图丙中画出在0～3s内，拉力F随时间t变化的图像。（不需要写出计算过程，只需写出表达式和画出图线）
参考答案：（1）1.2A（2）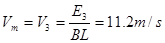
（3）
本题解析：（1）在0～1s时间内，cd杆向下做匀加速运动，由乙图可知：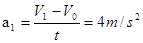
?（1）?（1分）
对cd杆进行受力分析，根据牛顿第二定律有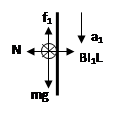
在竖直方向上：?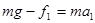
?（2）?（1分）
在水平方向上：?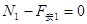
?
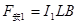
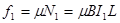?（3）?（2分）
由（2）和（3）式可得：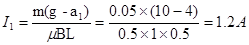 
?（4）式?（2分）
（2）在2～3s时间内，cd杆向下做匀减速运动时，由乙图可知：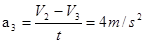
?（5）式?（2分）
对cd杆进行受力分析，根据牛顿第二定律有
在竖直方向上：?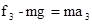
?（6）式?（2分）
在水平方向上：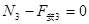 
?
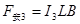
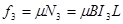?（7）式?
由（6）和（7）式可得：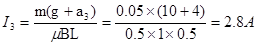 
?（2分）
所以电动势?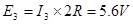
?（8）式?（1分）
又因为?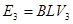
所以ab杆的最大速度为：?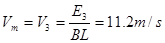
（9）式?（1分）
（3）解法提示：
在0~1.0s内，ab杆做匀速运动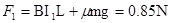
?
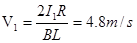?(1分)
在2.0~3.0s内，ab杆做匀速运动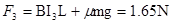
?
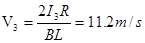?(1分)
在1~2s内，ab杆做匀加速运动，加速度为 
?(1分)
对ab杆分析，根据牛顿第二定律有：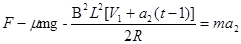
? (1s<t<2s)
所以表达式为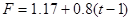
(1s<t<2s) （10）式（2分）
当t=1s时拉力为?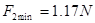
当t=2s时拉力为?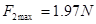
在0～3.0s内，拉力F随时间t变化的图像见图（3分）
本题考查电磁感应中切割磁感线的应用，首先根据图像求得加速度，以cd杆为研究对象分析受力，由牛顿第二定律求出安培力从而求得电流大小，同理求得第二问，在第三问中以ab杆为研究对象，由于ab杆做匀速直线运动，受力平衡列式求解
本题难度：一般
4、计算题 在平面直角坐标系xOy中，第I象限存在沿y轴负方向的匀强电场，第Ⅳ象限存在垂直于坐标平面向外的匀强磁场，磁感应强度为B。一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场，经x轴上的N点与x轴正方向成θ=60°角射入磁场，最后从y轴负半轴上的P点垂直于y轴射出磁场，如图所示，不计粒子重力，求
(1)M、N两点间的电势差UMN；
(2)粒子在磁场中运动的轨道半径r；
(3)粒子从M点运动到P点的总时间t。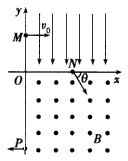
参考答案：解：(1)设粒子过N点时的速度为v，有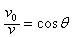
?①
v=2v0 ②
粒子从M点运动到N点的过程，有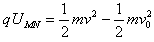
③
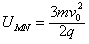?④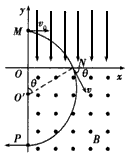 
(2)粒子在磁场中以O"为圆心做匀速圆周运动，半径为O"N，有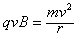
?⑤
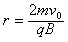?⑥
(3)由几何关系得ON=rsinθ ⑦
设粒子在电场中运动的时间为t1，有ON=v0t1 ⑧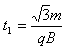
?⑨
粒子在磁场中做匀速圆周运动的周期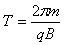
?⑩
设粒子在磁场中运动的时间为t2，有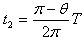
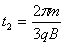
t=t1+t2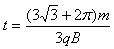
本题解析：
本题难度：困难
5、简答题 （14分）如图所示，坐标系xOy在竖直平面内，空间有沿水平方向、垂直纸面向外的匀强磁场，磁感应强度为B。在x>0的空间内有沿x轴正方向的匀强电场，场强为E。一个带正电荷的小球经过图中x轴上的M点，沿着与水平方向成θ=30?角的斜向下的直线做匀速运动，经过y轴上的N点进入x<0的区域内。要使小球进入x<0区域后能在竖直面内做匀速圆周运动，需在x<0区域内另加一匀强电场。若带电小球做圆周运动通过y轴上的P点（P点未标出），重力加速度设为g，求
：
（1）小球运动的速度大小；
（2）在x<0的区
域内所加电场的场强大小和方向；
（3）小球从N点运动到P点所用的时间。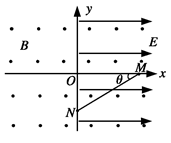
参考答案：（1）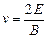
（2）
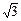E，方向为竖直向上。
（3）
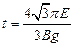
本题解析：（1）（4分）球在MN段受力如图：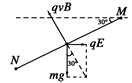
因为在MN段球做匀速直线运动，所以球受到如图所示的三个力而平衡，
所以有：mgtan30° ＝qE
qvBsin30
°＝qE
联立解得：mg=３qE；；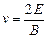
（２）（4分）在x＜０的区域内,设所加的电场强度为E′，则由运动情况分析知：
球受的重力mg必与电场力qE′是一对平衡力，即：qE′＝mg
∴?Eˊ = mg/q =E ；
E′的方向为竖直向上。
（３）（4分）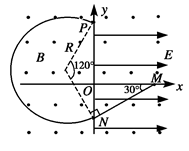
球在磁场中做匀速圆周运动的周期是：
Ｔ＝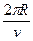
而：qvB＝m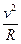
∴
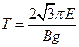
∴?在NP圆弧间经历的时间是：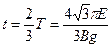
本题难度：一般