时间:2018-03-18 09:56:38
1、计算题 (12分)如下图所示,初速度为零的负离子经电势差为U的匀强电场加速后,从离子枪T
中水平射出,经过一段路程后进入水平放置的距离为d的两平行金属板MN和PQ之间,
离子所经空间存在着磁感应强度为B的匀强磁场.不考虑离子重力作用,离子的荷质比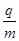 在什么范围内,离子才能打在金属板PQ上?
在什么范围内,离子才能打在金属板PQ上?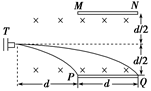
参考答案: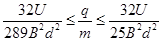
本题解析:在加速过程中,据动能定理有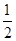 mv2=qU ①(2分)
mv2=qU ①(2分)
分析离子进入磁场后打到金属板两端的轨迹,如图所示,设半径分别为R1和R2,则离子打到金属板上的条件是R1≤R≤R2(2分)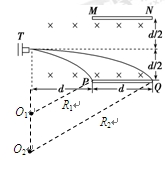
勾股定理知: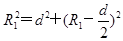 ?②(1分)
?②(1分)
由②式解得R1=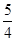 d ③
d ③
同理可得:R22=(2d)2+(R2-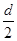 )2?④(1分)
)2?④(1分)
由④式解得:R2=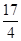 d ⑤
d ⑤
离子在磁场中运动时,由洛仑兹力和向心力公式可得: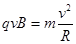 ?⑥(1分)
?⑥(1分)
由⑥式解得: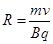 ?⑦(1分)
?⑦(1分)
由①⑦式解得: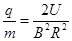 ?⑧(2分)
?⑧(2分)
因R1≤R≤R2 由③⑤⑧可得: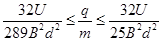 ?⑨(2分
?⑨(2分
本题难度:一般
2、计算题 如图所示,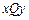 是位于足够大的绝缘光滑水平桌面内的平面直角坐标系,虚线MN是∠
是位于足够大的绝缘光滑水平桌面内的平面直角坐标系,虚线MN是∠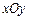 的角平分线.在MN的左侧区域,存在着沿
的角平分线.在MN的左侧区域,存在着沿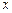 轴负方向、场强为E的匀强电场;在MN的右侧区域,存在着方向竖直向下、磁感应强度为B的匀强磁场,现有一带负电的小球
轴负方向、场强为E的匀强电场;在MN的右侧区域,存在着方向竖直向下、磁感应强度为B的匀强磁场,现有一带负电的小球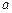 从y轴上的P(0,L)点,在电场力作用下由静止开始运动,小球
从y轴上的P(0,L)点,在电场力作用下由静止开始运动,小球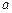 到达虚线MN上的Q点时与另一个不带电的静止小球
到达虚线MN上的Q点时与另一个不带电的静止小球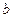 发生碰撞,碰后两小球粘合在一起进入磁场,它们穿出磁场的位置恰好在O点.若
发生碰撞,碰后两小球粘合在一起进入磁场,它们穿出磁场的位置恰好在O点.若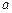 、
、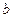 两小球的质量相等且均可视为质点,
两小球的质量相等且均可视为质点,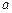 、
、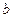 碰撞过程中无电荷量损失,不计重力作用.求:
碰撞过程中无电荷量损失,不计重力作用.求:
(1)小球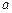 的比荷
的比荷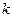 (即电荷量与质量之比);
(即电荷量与质量之比);
(2)过O点后,粘在一起的两个小球再次到达虚线MN上的位置坐标(结果用E、B、L表示).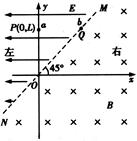
参考答案:(1)设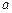 的质量为
的质量为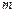 、电荷量为
、电荷量为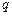 ,
,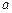 与
与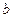 碰撞前后的速度大小分别为
碰撞前后的速度大小分别为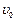 、
、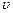 ,碰后两球在磁场中运动的轨道半径为R.
,碰后两球在磁场中运动的轨道半径为R.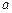 在电场中做匀加速直线运动,由动能定理得:
在电场中做匀加速直线运动,由动能定理得: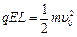 (2分)
(2分) 与
与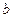 碰撞中动量守恒,有:
碰撞中动量守恒,有: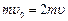 (2分)解得
(2分)解得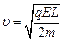 (2分)
(2分)
由题意知,Q点的位置坐标一定是(L,L),且碰后两球在磁场中做匀速圆周运动的圆心O1一定在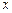 轴上,如图,所以R=L(2分)由洛伦兹力提供向心力有:
轴上,如图,所以R=L(2分)由洛伦兹力提供向心力有: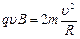 (2分)故有
(2分)故有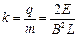 (2分)
(2分)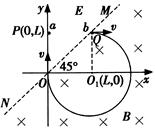
(2)过O点后,两球以沿 轴正方向的初速度
轴正方向的初速度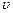 在电场中做类平抛运动,设它们再次到达虚线MN上的位置坐标为
在电场中做类平抛运动,设它们再次到达虚线MN上的位置坐标为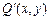 ,在电场中运动的时间为
,在电场中运动的时间为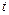 由运动学公式的:
由运动学公式的: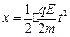 (2分)
(2分)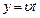 (2分)且
(2分)且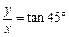 (2分)解得:
(2分)解得: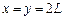 ,所以两球再次到达虚线MN上的位置坐标是
,所以两球再次到达虚线MN上的位置坐标是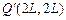
本题解析:略
本题难度:一般
3、填空题 如图所示,长度为l的绝缘轻杆一端可绕O点在竖直平面内自由转动,另一端固定一个质量为m、带电量为+q的小球,整个装置处于水平向右的匀强电场中,电场强度E=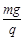 。现将小球从最低点A处由静止释放,则轻杆可以转过的最大角度为_____________。若在轻杆的中点施加一个始终垂直于杆的作用力F,F的大小始终保持为2mg,将小球从图中的B处由静止释放后,作用力F的最大功率Pm=_____________。
。现将小球从最低点A处由静止释放,则轻杆可以转过的最大角度为_____________。若在轻杆的中点施加一个始终垂直于杆的作用力F,F的大小始终保持为2mg,将小球从图中的B处由静止释放后,作用力F的最大功率Pm=_____________。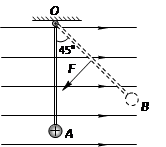
参考答案:90°,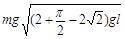 或0.86mg
或0.86mg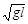 ?(每空2分)
?(每空2分)
本题解析:因为电场强度E=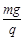 ,杆平衡位置处于与竖直夹角45°的B位置,将小球从最低点A处由静止释放,当电场做功等于重力势能时,轻杆转过的角度最大,此时关于B点对称,则轻杆可以转过的最大角度为90°;
,杆平衡位置处于与竖直夹角45°的B位置,将小球从最低点A处由静止释放,当电场做功等于重力势能时,轻杆转过的角度最大,此时关于B点对称,则轻杆可以转过的最大角度为90°;
本题难度:简单
4、计算题 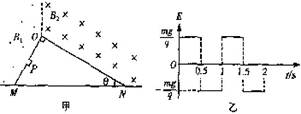 25.(17分)如图甲所示,光滑、绝缘直角三角型斜面
25.(17分)如图甲所示,光滑、绝缘直角三角型斜面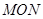 固定在水平地面上,
固定在水平地面上,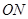 边长
边长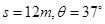 ;虚线左、右空间存在
;虚线左、右空间存在
磁感应强度为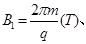 ?
?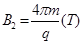 的匀强磁场,方向分别垂直于纸面向里、向外;整个空间存在着竖直方向的、随时问交替变化的匀强电场(如图乙所示,竖直向上方向为正方向)。在距
的匀强磁场,方向分别垂直于纸面向里、向外;整个空间存在着竖直方向的、随时问交替变化的匀强电场(如图乙所示,竖直向上方向为正方向)。在距 点
点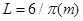 处的
处的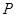 点有一物块抛射器,在
点有一物块抛射器,在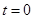 时刻将一质量为
时刻将一质量为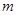 、带电荷量为
、带电荷量为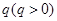 的小物块(可视为质点)抛入电磁场,小物块恰好能在
的小物块(可视为质点)抛入电磁场,小物块恰好能在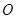 点切入
点切入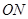 斜面。设小物块在
斜面。设小物块在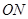 面上滑行时无电荷损失且所受洛伦兹力小于
面上滑行时无电荷损失且所受洛伦兹力小于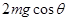 ,求:
,求:
(1)小物块抛出速度的大小;
(2)小物块从抛出到运动至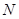 点所用时间。
点所用时间。
参考答案:
(1)6m/s
(2)2s
本题解析:解:(1)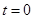 时刻小物块进入电磁场,由乙图知,电场方向向上,且有
时刻小物块进入电磁场,由乙图知,电场方向向上,且有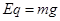 ,所以小物块在洛伦兹力作用下做匀速圆周运动(1分)
,所以小物块在洛伦兹力作用下做匀速圆周运动(1分)
小物块恰好由 点切入斜面,小物块被抛出时的速度方向必垂直于
点切入斜面,小物块被抛出时的速度方向必垂直于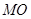 ,设此过程中小物块运动的时间为
,设此过程中小物块运动的时间为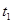 ,有
,有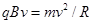 ?(2分)?
?(2分)?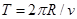 ?(2分)
?(2分)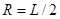 ? (1分)?
? (1分)?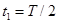 ?(2分)
?(2分)
代入数据解得,小物块的抛出速度的大小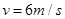 ,运动周期
,运动周期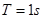 ,
,
在磁场 中运动的时间
中运动的时间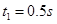 ? (1分)
? (1分)
(2)小物块切入 时,电场方向变为向下,有
时,电场方向变为向下,有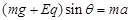 ,将
,将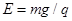 代入,
代入,
解得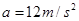 ? (2分)
? (2分)
当电场变为竖直向上后小物块正好做一个完整的圆周运动,然后电场方向又变为竖直向下,小物块继续沿斜面以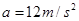 的加速度下滑,故设小物块在斜面上滑行的总时间为
的加速度下滑,故设小物块在斜面上滑行的总时间为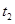 ,则有
,则有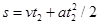 ? (2分)
? (2分)
代入数据得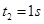 ?(
?(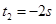 舍去)? (1分)
舍去)? (1分)
分析知,小物块沿斜面下滑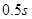 后,作一个完整的圆周运动,然后又沿斜面下滑
后,作一个完整的圆周运动,然后又沿斜面下滑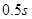 到达
到达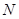 点,设做周运动的时间是
点,设做周运动的时间是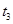 ,因为
,因为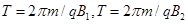 ,又
,又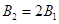 ,所以
,所以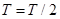 ,则
,则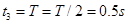 ? (2分)
? (2分)
小物块从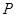 点运动到
点运动到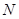 点所用时间为
点所用时间为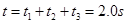 ? (1分)
? (1分)
本题难度:一般
5、简答题 如图所示,电源电动势E=3V,内阻r=2Ω。半径R=0.1m的圆形区域内有匀强磁场垂直纸面向外,磁感应强度B=0.1T。竖直平行正对放置的两金属板连在可调电路中,S1、S2为A、K板上的两个小孔,且与O在同一水平直线上。今有一荷质比为1.0×104C/㎏、带正电的粒子由S1进入电场,当滑动变阻器R0的滑片P位于滑动变阻器的中点时,粒子垂直打在水平放置的荧光屏DQ的M点。不计粒子的重力及粒子进入电场的速度,求此时电源的输出功率及带电粒子打在M点时的速度。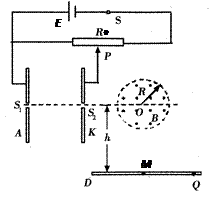


参考答案:(1) 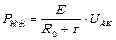 ?(2)?
?(2)?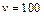 m/s
m/s
本题解析:由题意可知,带电粒子在A、K两个极板间做匀加速直线运动,进入圆形磁场区域后做四分之一圆周运动后飞出磁场,后做匀速直线运动打到M点。则:
由欧姆定律有: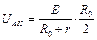 ? …………………①?
? …………………①?
对电源: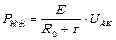 ? …………………②?
? …………………②?
带电粒子在极板间加速,由动能定理有: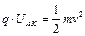 ? …………………③?
? …………………③?
带电粒子在磁场中做匀速圆周运动,牛顿第二定律有: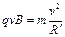 ? …………………④?
? …………………④?
由几何关系有: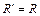 ? …………………⑤?
? …………………⑤?
联 www.91eXam.org解①②③④⑤得: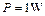 ?
?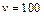 m/s
m/s
本题难度:一般