时间:2018-03-18 09:16:06
1、选择题 为了测定一个水平向右的匀强电场的场强大小,小明所在的物理兴趣小组做了如下实验:用长为L的细线,上端固定于O点,下端拴一质量为m、带电荷量为+q的小球,如图所示,开始时,将线与小球拉成水平,然后释放,小球由静止开始向下摆动,到B点时速度恰好为零,然后又从B点向A点摆动,如此往复。小明用测量工具测量与水平方向所成的角度 ,刚好为60°。下列说法中正确的是
,刚好为60°。下列说法中正确的是
A.在B点时小球受到的合力为0
B.小球从A运动到B,重力势能减小mgL
C.小球在下摆的过程中,小球的机械能和电势能之和先减小后增大
D.电场强度E的大小为 

2、选择题 如图所示,质量m=1kg、长L=0.8m的均匀矩形薄板静止在水平桌面上,其右端与桌子边缘相平.板与桌面间的动摩擦因数为μ=0.4.现用F=5N的水平力向右推薄板,使它翻下桌子,力F做的功至少为( )(g取10m/s2)
A.1J
B.1.6J
C.2J
D.4J
3、选择题 一物体沿直线运动,其v-t图象如图所示,已知在第1s内合外力对物体做功为W,则( )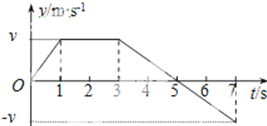
A.从第1s末到第2s末,合外力做功为2W
B.从第3s末到第5s末,合外力做功为W
C.从第5s末到第7s末,合外力做功为W
D.从第3s末到第7s末,合外力做功为W
4、选择题 如图甲所示,一质量为M=1kg的物块静止在粗糙水平面上的A点,从t=0时刻开始,物块在按如图乙所示规律变化的水平力F的作用下向右运动,第3s末物块运动到B点且速度刚好为0,第5s末物块刚好回到A点,物块与粗糙水平面间的动摩擦因数μ=0.2,g取10m/s2,则以下说法正确的是 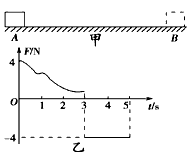
[? ]
A.物块在5s内克服摩擦力做功8J
B.第5s末,物块的动能为16J
C.水平力F在5s内对物块平均做功功率为3.2W
D.水平力F在3s内对物块所做的功为8J
5、选择题 如果物体的运动状态发生了变化,说明该物体的
A.速率一定发生了改变
B.惯性一定发生了改变
C.加速度一定发生了改变
D.受到的合外力一定不为零