时间:2018-03-18 09:05:02
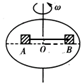
1、选择题 如图所示,在水平圆盘上沿半径方向放置用细线相连的质量均为m的A、B两个物块(可视为质点).?A和B距轴心O的距离分别为rA=R,rB=2R,且A、B与转盘之间的最大静摩擦力都是fm,两物块A和B随着圆盘转动时,始终与圆盘保持相对静止.则在圆盘转动的角速度从0缓慢增大的过程中,下列说法正确的是( )
A.B所受合外力一直等于A所受合外力
B.A受到的摩擦力一直指向圆心
C.B受到的摩擦力一直指向圆心
D.A、B两物块与圆盘保持相对静止的最大角速度
| 2fm mR |
参考答案:
A、A、B都做匀速圆周运动,合力提供向心力,根据牛顿第二定律得F合=mω2r,角速度ω相等,B的半径较大,所受合力较大.故A错误.
B、C最初圆盘转动角速度较小,A、B随圆盘做圆周运动所需向心力较小,可由A、B与盘面间静摩擦力提供,静摩擦力指向圆心.由于B所需向心力较大,当A与盘面间静摩擦力达到最大值时(此时B与盘面间静摩擦力还没有达到最大),若继续增大转速,则B将做离心运动,而拉紧细线,使细线上出现张力,转速越大,细线上张力越大,使得B与盘面间静摩擦力增大,当B与盘面间静摩擦力也达到最大时,B将开始滑动,A所受的静摩擦力将离开圆心.所以A受到的摩擦力先指向圆心,后离开圆心,而B受到的摩擦力一直指向圆心.故B错误,C正确.
D、当B与盘面间静摩擦力恰好达到最大时,B将开始滑动,则根据牛顿第二定律得
? 对A:T-fm=mω2mr
?对B:T+fm=mω2m?2r
解得最大角速度ωm=2fmmR.故D正确.
故选CD
本题解析:
本题难度:简单
2、选择题 如图所示,自由下落的小球,从它接触竖直放置的弹簧开始到弹簧压缩到最短的过程中,小球的加速度和速度的变化情况是 
A.加速度变小,速度变小
B.加速度变大,速度变小
C.加速度先变小后变大,速度先变大后变小
D.加速度先变大后变小,速度先变大后变小
参考答案:C
本题解析:开始阶段,弹簧的压缩量较小,因此弹簧对小球向上的弹力小于向下重力,此时合外力大小:F=mg-kx,方向向下,随着压缩量的增加,弹力增大,故合外力减小,则加速度减小,由于合外力与速度方向相同,小球的速度增大;当mg=kx时,合外力为零,此时速度最大;由于惯性物体继续向下运动,此时合外力大小为:F=kx
本题难度:一般
3、选择题 关于匀速圆周运动的向心力, 下列说法中正确的是
[? ]
A.匀速 圆周运动中向心力是恒力
圆周运动中向心力是恒力
B.匀速圆周运动的向心力是大小不变、方向变化的变力
C.匀速圆周运动的向心力的功率是零
D.匀速圆周运动的向心力一定是物体受到的合力
参考答案:BCD
本题解析:
本题难度:简单
4、选择题 如图,一束电子以大小不同的速率沿图示方向飞人一正方形的匀强磁场区,对从油边离开磁场的电子,下列判断正确的是( )
A.从a点离开的电子速度最小
B.从a点离开的电子在磁场中运动时间最短
C.从b点离开的电子运动半径最小
D.从b点离开的电子速度偏转角最小
参考答案:对于从右边离开磁场的电子,从a离开的轨道半径最大,根据带电粒子在匀强磁场中的半径公式r=mvqB,知轨道半径大,则速度大,则a点离开的电子速度最大.从a点离开的电子偏转角最小,则圆弧的圆心角最小,根据t=θ2πT=θ2π?2πmqB=θmqB,与粒子的速度无关,知θ越小,运行的时间越短.故B、C正确,A、D错误.
故选BC.
本题解析:
本题难度:一般
5、选择题 如图所示,用细线吊着一个质量为m的小球,使小球在水平面内做圆锥摆运动,关于小球受力的说法,正确的是( )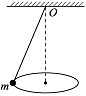
A.受重力、拉力、向心力
B.受重力、拉力
C.只受重力
D.以上均不对
参考答案:B
本题解析:小球受重力、和绳子的拉力,由于它们的合力总是指向圆心并使得小球在水平面内做圆周运动,故在物理学上,将这个合力就叫做向心力,即向心力是按照力的效果命名的,这里是重力和拉力的合力!故选B
点评:本题难度较小,向心力是效果力,匀速圆周运动中由合外力提供,是合力,与分力是等效替代关系,不是重复受力
本题难度:简单