时间:2017-11-10 09:10:34
1、计算题 （12分）如图所示，在x轴上方有垂直于x0y平面向里的匀强磁场，磁感应强度为B。在x轴下方有沿y轴负方向的匀强电场，场强为E，一质量为m，电荷量为-q的粒子从坐标原点沿着y轴正方向射出，射出之后，第三次到达x轴时，它与点O的距离为L，不计粒子所受重力。求：
（1）此粒子射出的速度v；
（2）运动的总路程X。
2、选择题 如图所示，半径为R的环形塑料管竖直放置，AB为该环的水平直径，且管的内径远小于环的半径，环的A、B及其以下部分处于水平向左的匀强电场中，管的内壁光滑。现将一质量为m，带电荷量为+q的小球从管中A点由静止释放，已知qE=mg，以下说法错误的是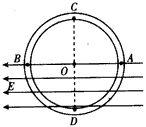
[? ]
A.小球释放后，到达B点时速度为零，并在BDA同往复运动
B.小球释放后，到达最低点D时速度最大
C.小球释放后，第一次和第二次经过最高点C时对管壁的压力大小之比为1:1且方向相同
D.小球释放后，第一次经过最低点D和最高点C时对管壁的压力大小之比为5:1
3、计算题 (12分)如图所示，在xoy平面内，直线MN与x轴正方向成30o角，MN下方是垂直于纸面向外的匀强磁场，MN与y轴正方向间存在电场强度E=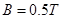
×105N/C的匀强电场，其方向与y轴正方向成60o角且指向左上方，一重力不计的带正电粒子，从坐标原点O沿x轴正方向进入磁场，已知粒子的比荷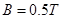=107C/kg，结果均保留两位有效数字，试问：
（1）若测得该粒子经过磁场的时间t1=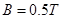，求磁感应强度的大小B；
（2）若测得该粒子经过磁场的时间t1=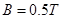，粒子从坐标原点开始到第一次到达y轴正半轴的时间t
（3）若粒子的速度v0=1.0×106m/s，求粒子进入电场后最终离开电场时的位置坐标
4、计算题 （20分）如图所示，一质量为m、电荷量为q、重力不计的微粒，从倾斜放置的平行电容器I的A板处由静止释放，A、B间电压为U1。微粒经加速后，从D板左边缘进入一水平放置的平行板电容器II，由C板右边缘且平行于极板方向射出，已知电容器II的板长为板间距离的2倍。电容器右侧竖直面MN与PQ之间的足够大空间中存在着水平向右的匀强磁场（图中未画出），MN与PQ之间的距离为L，磁感应强度大小为B，在微粒的运动路径上有一厚度不计的窄塑料板（垂直纸面方向的宽度很小），斜放在MN与PQ之间，
=45°。求：
（1）微粒从电容器I加速后的速度大小；
（2）电容器IICD间的电压；
（3）假设粒子与塑料板碰撞后，电量和速度大小不变、方向变化遵循光的反射定律，碰撞时间极短忽略不计，微粒在MN与PQ之间运动的时间和路程。
5、计算题 （16分）如图所示，宽度为L=1m的某一区域存在相互垂直的匀强电场E和匀强磁场B，其大小E=2×108N/C，B=1T。一带正电的粒子以基本一初速度由M点垂直电场和磁场进入，沿直线从N点离开；若只撤去磁场，则粒子从P与水平成450角射出。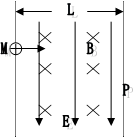
（1）求粒子的比荷
（2）若只撤去电场，则粒子以与水平方向成多少度角穿出