时间:2017-11-10 08:48:21
1、简答题 一名宇航员在登陆某星球后为了测量此星球的质量进行了如下实验:他把一小钢球托举到距星球表面高度为?h?处由静止释放,计时仪器测得小钢球从释放到落回星球表面的时间为t.此前通过天文观测测得此星球的半径为?R,已知万有引力常量为G,不计小钢球下落过程中的气体阻力,可认为此星球表面的物体受到的重力等于物体与星球之间的万有引力.求:
(1)此星球表面的重力加速度?g;
(2)此星球的质量?M;
(3)若距此星球表面高?H?的圆形轨道有一颗卫星绕它做匀速圆周运动,求卫星的运行周期?T.
参考答案:(1)由h=12gt2得,g=2ht2.
(2)根据GMmR2=mg
解得M=gR2G=2hR2Gt2.
(3)根据万有引力提供向心力得,GMm(R+H)2=m(R+H)(2πT)2
又GM=gR2
解得T=
本题解析:
本题难度:一般
2、简答题 “嫦娥一号”探月卫星与稍早前日本的“月亮女神号”探月卫星不同,“嫦娥一号”卫星是绕月极地轨道上运动的,加上月球的
自转,因而“嫦娥一号”卫星能探测到整个月球的表面.12月11日“嫦娥一号”卫星CCD相机已对月球表面进行成像探测,并获取了月球背面部分区域的影像图.卫星在绕月极地轨道上做圆周运动时距月球表面高为H,绕行的周期为TM;月球地公转的周期为TE,半径为R0.地球半径为RE,月球半径为RM.试解答下列问题:
(1)若忽略地球及太阳引力对绕月卫星的影响,试求月球与地球质量之比;
(2)当绕月极地轨道的平面与月球绕地公转的轨道平面垂直,也与地心到月心的连线垂直(如图所示).此时探月卫星向地球发送所拍摄的照片,此照片由探月卫星传送到地球最少需要多长时间?已知光速为c.
参考答案:(1)由牛顿第二定律得F向=man=m(2πT)2r
月球绕地公转由万有引力提供向心力得,GM月M地R20=M月(2πTE)2R0
同理,探月卫星绕月运动时有:GM月M卫(RM+H)2=M卫(2πTM)2(RM+H)
由上两式联立解得:M月M地=(TETM)2×(RM+HR0)3;
(2)设探月极地轨道上卫星到地心的距离为L0,则卫星到地面最短距离为L0-RE,由几何知识得:
? L02=R02+(RM+H)2
将照片发回地面的时间
t=L0-REc=
本题解析:
本题难度:一般
3、简答题 如图所示,长为L=0.5m的轻杆OA绕O点在竖直平面内做匀速圆周运动,A端连着一个质量为m=2kg的小球,取g=10m/s2.
(1)如果小球的速度为3m/s,求在最低点时杆对小球的拉力为多大?
(2)如果在最高点杆对小球的支持力为4N,求杆旋转的角速度为多大?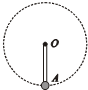
参考答案:(1)小球在最低点,根据向心力公式得:
T-mg=mv2L
解得:T=2×90.5+20=56N
(2)小球在最高点,根据向心力公式得:
mg-N=mω2L
解得:ω=4rad/s
答:(1)如果小球的速度为3m/s,在最低点时杆对小球的拉力为56N;
(2)如果在最高点杆对小球的支持力为4N,杆旋转的角速度为4rad/s.
本题解析:
本题难度:一般
4、选择题 乘坐如图所示游乐园的过山车时,质量为m的人随车在竖直平面内沿圆周轨道运动,下列说法正确的是( )
A.车在最高点时人处于倒坐状态,全靠保险带拉住,若没有保险带,人一定会掉下去
B.人在最高点时对座位仍可能产生压力,且压力不一定小于mg
C.人在最高点和最低点时的向心加速度大小相等
D.人在最低点时对座位的压力大于mg
参考答案:A、当人与保险带间恰好没有作用力,由重力提供向心力时,临界速度为v0=
本题解析:
本题难度:简单
5、选择题 一个带电粒子在磁场中运动,某时刻速度方向如图,受到的重力和洛仑磁力的合力的方向恰好与速度方向相反,不计阻力,那么接下去的一小段时间内,带电粒子( )
A.可能作匀减速运动
B.不可能作匀减速运动
C.可能作匀速直线运动
D.不可能做匀速直线运动
参考答案:A、B匀减速运动的合外力应该恒定不变.带电粒子在磁场中受到重力和洛伦兹力两个力作用,而洛伦兹力的大小与速度大小成正比,若减速,则其洛伦兹力将减小,粒子的合外力 将发生变化,不再恒定,所以不可能做匀减速运动.故A错误,B正确.
C、D若要做匀速直线运动,重力和洛伦兹力必须平衡,大小相等,方向相反,由图可知洛伦兹力方向斜向左上方,与重力方向不在同一直线上,两者不可能平衡,则不可能做匀速直线运动.故C错误,D正确.
故选BD
本题解析:
本题难度:一般