时间:2017-11-10 08:09:07
1、选择题 对于安培力和洛仑兹力,以下说法正确的是
A.通电导线在磁场中一定受安培力
B.只有通电导线与磁场垂直时才受安培力
C.不管带电粒子做什么运动,洛仑兹力总不做功
D.只有带电粒子在匀强磁场中做匀速圆周运动时,洛仑兹力才不做功
参考答案:C
本题解析:安培力是指电流受到的磁场力,必须是电流与磁场有夹角,所以AB错;
带电粒子只有运动时,且与磁场夹角不为零时才受力,力与速度垂直,不做功,所以C对,D错。
本题难度:简单
2、填空题 如图所示,通电直导线右边有一个矩形线框,线框平面与直导线共面,若使其逐渐远离(平动)通电导线,则穿过线框的磁通量将______?(填写“逐渐减小”或者“逐渐增大”、“保持不变”)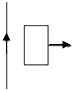
参考答案:由题,通电直导线产生稳定的磁场,离导线越远磁场越弱,磁感线越疏,则当线框远离通电导线时,穿过线框的磁感线的条数越来越少,磁通量将逐渐减小.
故答案为:逐渐减小
本题解析:
本题难度:一般
3、选择题 把一个可以绕水平轴转动的铝盘放在水平方向的匀强磁场中,匀强磁场的方向与铝盘平面垂直,盘的下边浸在水银槽内,将转轴和水银用导线直接连在电源的两极上,如图所示,则下列说法正确的是( )
A.由于磁场对电流的作用,铝盘将顺时针转动
B.由于磁场对电流的作用,铝盘将逆时针转动
C.将电源两极对调,铝盘的转动方向不会改变
D.将电流及磁场方向同时改变,铝盘的转动方向改变
参考答案:A、铝盘、水银与电源构成一个闭合回路,铝盘中有电流,由左手定则可知:铝盘受到的安培力与盘的半径垂直,且沿逆时针方向,则铝盘沿逆时针方向转动,故A错误,B正确;
C、将电源两极对调,电流方向反向,由左手定则可知,安培力方向反向,铝盘的转动方向反向,故C错误;
D、由左手定则可知,将电流及磁场方向同时改变,铝盘受力方向不变,铝盘的转动方向不变,故D错误;
故选B.
本题解析:
本题难度:一般
4、填空题 图中+q受洛仑兹力,(1)水平向外的是图 ;(2)竖直向上的是图 ;(3)竖直向下的是图 。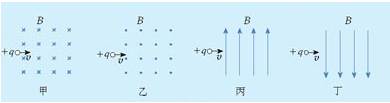
参考答案:(1) 丙;(2) 甲 ;(3) 乙。
本题解析:略
本题难度:一般
5、选择题 如图,一段导线abcd位于磁感应强度大小为B的匀强磁场中,且与磁场方向(垂直于纸面向里)垂直。线段ab、be和cd的长度均为L,且∠abc=∠bcd= 135°。流经导线的电流为I,方向如图中箭头所示。导线段abcd所受到的磁场的作用力的合力
[? ]
A.方向沿纸面向上,大小为
B.方向沿纸面向上,大小为
C.方向沿纸面向下,大小为
D.方向沿纸面向下,大小为
参考答案:A
本题解析:
本题难度:一般