时间:2017-11-10 07:58:53
1、填空题 一小船与船上人的总质量为160kg，以2m/s的速度匀速向东行驶，船上一个质量为60kg的人，以6m/s的水平速度（相对跳离时小船的速度）向东跳离此小船，若不计水的阻力，则人跳离后小船的速度大小为_________m/s，小船的运动方向为向______。
参考答案：0.25；向西
本题解析：
本题难度：一般
2、计算题 如图所示，质量分别为
、
的两个小物块静止在光滑的水平面上，彼此用轻弹簧相连，弹簧处于自由伸长状态。质量为
的子弹以速度为
水平入射到
物块内（子弹未射出），试求：
（1）子弹打入
后，
的速度；
（2）弹簧压缩到最短时，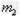
的速度；
（3）整个运动过程中，弹簧的最大弹性势能为多少？（弹簧始终在弹性限度范围内）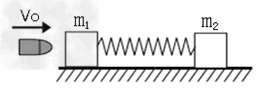
参考答案：解：（1）子弹打木块的过程，由动量守恒，得：
解得：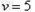
m/s
（2）m1与m2压缩弹簧的过程，整体动量守恒，知：
弹簧压缩到最短时，满足：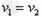
解得：
m/s
（3）弹簧压缩到最短时，弹性势能最大，由机械能守恒，知：
解得：
本题解析：
本题难度：一般
3、简答题 处于静止状态的某原子核X，发生α衰变后变成质量为M的原子核Y，被释放的α粒子垂直射人磁感强度为B的匀强磁场中，测得其圆周与运动的半径为r，设α粒子质量为m，质子的电量为e，试求：
（1）衰变后α粒子的速率υa和动能Eka；
（2）衰变后Y核的速率υy和动能Eky；
（3）衰变前X核的质量Mx．
参考答案：（1）α粒子在匀强磁场中做圆周与运动所需的向心力同洛仑兹力提供，
即Bqv=mv2αr，α粒子的带电量为q=2e
所以α粒子的速率：vα=2Berm，
动能：Ekα=12mv2α=2B2e2r2m
（2）由动量守恒mvα-Mvy=0
所以vy=2Berm，
Eky=12Mv2y=2B2e2r2M
（3）由质能方程：△E=△mc2，
而△E=Ekx+Eky，
所以△m=2B2e2r2c2（1m+1M）
衰变前X核的质量：Mx=m+M+△m=m+M+2B2e2r2c2（1m+1M）．
答：（1）衰变后α粒子的速率υa为2Berm，动能Eka为2B2e2r2m；
（2）衰变后Y核的速率υy为=2Berm，动能Eky为2B2e2r2M；
（3）衰变前X核的质量Mx为m+M+2B2e2r2c2（1m+1M）．
本题解析：
本题难度：一般
4、选择题 在光滑的水平面上有a、b两球，其质量分别是ma、mb，两球在t1时刻发生正碰，并且在碰撞过程中无机械能损失，两球在碰撞前后的速度图象如图所示．下列关系正确的是（?）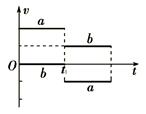
A．ma>mb
B．ma<mb
C．ma＝mb
D．无法判断
参考答案：B
本题解析：由图像可知碰前a球速度为2v，b球速度为零，碰后a速度反向，大小等于b球速度，由动量守恒和机械能守恒
可求出ab两球的质量之比，B对；
本题难度：简单
5、计算题 【物理—选修3-5模块】
（1）如图为氢原子的能级图，一群氢原子在n=4的定态发生跃迁时，能产生?种不同频率的光，其中产生的光子中能量最大是?ev
（2）下列核反应中，X1是?、X2是?，其中发生核裂变反应的是?。
①?
②?
（3）如图示，质量为m1=1kg和m2=2kg的两个小球在光滑的水平面上分别以V1=2m/s和V2=0．5m/s的速度相向运动，某时刻两球发生碰撞，碰后m1以1m/s的速度被反向弹回，求：
①碰后m2的速度
②两球发生碰撞的过程中m1受到的冲量
参考答案：（1）6、12.75ev（2）中子、氘核（用符号书写也给分）、①（3）1m/s方向向右、3NS 方向向左
本题解析：（1）从4到3，从4到2，从4到1，从3到2，从3到1，从2到1，共6种跃迁方式，所以产生6种不同频率的光，其中光子能量最大的是从4到1，即
(2)根据质量数和电荷数守恒可得
，所以X1是中子，
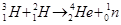，所以X2是氘核
（3）两球碰撞过程中动量守恒，以向右正方向，则
，解得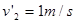
，方向向右，
根据冲量定理可得
，方向向左，
点评：做本题的关键是是理解相应的原理，特别是在书写核反应方程时，不能写等号，要写箭头，
本题难度：简单