时间:2017-11-10 07:32:14
1、简答题 飞机做特技时常做俯冲拉起运动.如图所示.此运动在最低点附近可看作是半径为1000m的圆周运动.若飞行员的质量为68kg,飞机经过最低点时的速度为360km/h,则这时飞行员对坐椅的压力为多大?g=10m/s2.
参考答案:飞机的速度v=360km/h=100m/s,设座椅对飞行员的弹力为N,飞行员的质量为m,
根据牛顿第二定律得:N-mg=mv2R
解得:N=mg+mv2R=68×10+68×100001000N=1360N.
由牛顿第三定律得,飞行员对座椅的压力为1360N.
答:这时飞行员对坐椅的压力为1360N.
本题解析:
本题难度:一般
2、选择题 如图所示,在y>0的区域内存在匀强磁场,磁场垂直于图中的Oxy平面,方向指向纸外,原点O处有一离子源,在Oxy平面内沿各个方向射出动量相等的同价负离子,对于进入磁场区域的离子,它们在磁场中做圆弧运动的圆心所在的轨迹,可用下图四个半圆中的一个来表示,其中正确的是( )
A.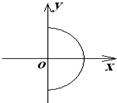
B.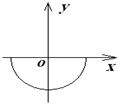
C.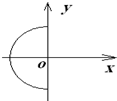
D.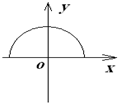
参考答案:由r=mvqB知,在磁场中做匀速圆周运动的所有粒子半径相同.由左手定则,分别研究离子沿x轴负方向、y轴正方向、x轴正方向射入的粒子,其分别在y轴负方向上、x轴负方向上和y轴正方向上,则知其做圆弧运动的圆心轨迹为C.故C正确.
故选C
本题解析:
本题难度:一般
3、选择题 人造地球卫星所受的向心力与轨道半径r的关系,下列说法中正确的是
[? ]
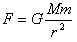 可知,向心力与r2成反比
可知,向心力与r2成反比 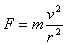 可知,向心力与r成反比
可知,向心力与r成反比 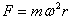 可知,向心力与r成正比
可知,向心力与r成正比 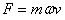 可知,向心力与r无关
可知,向心力与r无关 参考答案:A
本题解析:
本题难度:简单
4、简答题 如图所示,空间内存在水平向右的匀强电场,在虚线MN的右侧有垂直纸面向里、磁感应强度为B的匀强磁场,一质量为m、带电荷量为+q的小颗粒自A点由静止开始运动,刚好沿直线运动至光滑绝缘的水平面C点,与水平面碰撞的瞬间小颗粒的竖直分速度立即减为零,而水平分速度不变,小颗粒运动至D处刚好离开水平面,然后沿图示曲线DP轨迹运动,AC与水平面夹角α=30°,重力加速度为g.求: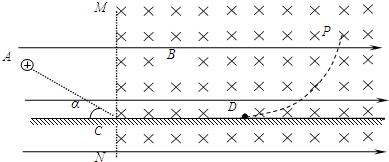
(1)匀强电场的场强E.
(2)AD之间的水平距离d.
(3)已知小颗粒在轨迹DP上某处的最大速度为vm,该处轨迹的曲率半径是距水平面高度的k倍,则该处的高度为多大?
参考答案:(1)小球受力如图所示: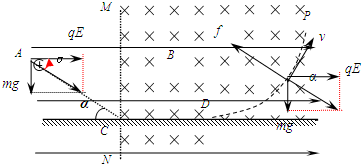
? qE=mgcotα?解得:E=
本题解析:
本题难度:一般
5、选择题 长为l轻杆的一端连接一个小球,另一端可以绕光滑水平轴在竖直平面内转动,则下列说法正确的是( )
A.小球在最高点时的速度一定大于或等于
| gl |
| 2gl |
参考答案:A、小球在最高点的最小速度为零.故A错误.
B、在最高点,v由
本题解析:
本题难度:简单