时间:2017-11-05 17:30:01
1、填空题 把物体竖直地挂在劲度系数为1000N/m的弹簧下端，弹簧伸长2cm。如果把物体放在动摩擦因数为0.30的水平地面上，用同一根弹簧沿水平方向拉物体。当物体产生2m/s2的加速度时，弹簧伸长?cm。
参考答案：1cm
本题解析：把物体竖直地挂在劲度系数为1000N/m的弹簧下端，弹簧伸长2cm。根据公式
可得
，当此物体在水平面上加速运动时
，当物体产生2m/s2的加速度时，弹簧伸长
本题难度：简单
2、计算题 (20分) 一传送带装置示意图如图，其中传送带AB段是水平的，CD段是倾斜的，动摩擦因数均为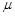
，AB段和CD段通过极短的BC段平滑连接．现将大量的质量均为m的小货箱一个一个在A处放到传送带上，放置时初速为零，经传送带运送到D处，D和A的高度差为h．稳定工作时传送带速度保持不变，始终为v，CD段上各箱等距排列，相邻两箱的距离为L．每个箱子在A处投放后，在到达B之前已经相对于传送带静止，且以后也不再滑动（忽略经BC段时的微小滑动）．传送带由电动机带动，传送带与轮子间无相对滑动，不计轮轴处的摩擦．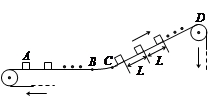
（1）为了小货箱到达B点前相对于传动带静止，AB段至少多长？
（2）将每个小货箱从A点运送到D点，因摩擦产生了多少热量？
（3）求电动机的平均输出功率？
参考答案：（1）
；（2）
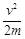；（3）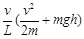
。
本题解析：(1)直接运用动能定理求解：
刚开始小货箱相对于传送带有滑动，相对静止前，设货箱在传送带上滑行的距离为s，
由动能定理得：
，解之得
。
也可以运用运动学的知识求解：
货箱的加速度a=gμ，加速到速度为v时的时间为t=
；
传送带运动的距离为s1=vt=
，货箱前进的距离为s2=
at2=
所以货箱在传送带上相对滑动的距离为s=s1－s2=－=。
(2) 每个小货箱从A点运送到D点只有在货箱与传送带发生相对运动时才产生热量，热量的大小等于摩擦力与相对运动距离的乘积。
Q=W=fs=mgμ×
(3) 设T时间内运送货箱N个,，则
每个货箱由A点运到D点需要能量E
故
，故电动机的平均输出功率P=
。
本题难度：一般
3、填空题 (2分) 如图所示的装置可以测量小车在水平路面上做匀变速直线运动的加速度．该装置是在车箱前、后壁各安装一个压力传感器a和b，中间用两根相同的轻质弹簧压着一个质量为4.0kg的滑块，滑块可无摩擦滑动．小车静止时，传感器a、b的读数均为10N．若当传感器a的读数为7N时，小车运动加速度的方向是? （填“向左”或“向右”），加速度大小为? m/s2．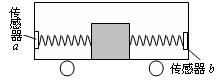
参考答案：向左；1.5 m/s2
本题解析：由题意可知，两弹簧的总伸长量不变，结合胡克定律可知，当a传感器计数为7N时，b传感器的计数为13N，弹簧处于压缩状态，故合力向左，由牛顿第二定律得Fb-Fa=ma，解得a=1.5m/s，方向向左。
本题难度：简单
4、计算题 如图所示，均可视为质点的三个物体A、B、C穿在竖直固定的光滑绝缘轻杆上，A与B紧靠在一起（但不粘连），C紧贴着绝缘地板，质量分别为MA=2.32kg，MB=0.20kg，MC=2.00kg，其中A不带电，B、C的带电量分别为qB = +4.0×10-5C，qC =+7.0×10-5C，且电量都保持不变，开始时三个物体均静止。现给物体A施加一个竖直向上的力F，若使A由静止开始向上作加速度大小为a=4.0m/s2的匀加速直线运动，则开始需给物体A施加一个竖直向上的变力F，经时间t 后， F变为恒力。已知g=10m/s2，静电力恒量k=9×109N·m2/c2，
求：（1）静止时B与C之间的距离；
（2）时间t的大小；
（3）在时间t内，若变力F做的功WF=53.36J，则B所受的电场力对B做的功为多大？
参考答案：（1）1.0m（2）1s（3）17.2J
本题解析：（1）开始时A、B处于平衡状态，设
之间的距离为
，则
，代入数据可得：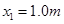
经时间t ， F变为恒力。A、B恰好分离，A、B间无相互作用，设BC之间的距离为
则
，代入数据可得：
(2) 
则，代入数据可得
(3) 以AB为系统，由动能定理可得
而
代入数据可得：
本题难度：一般
5、计算题 （14分）如图所示，半径R＝0.8 m的光滑圆弧轨道固定在水平地面上，O为该圆弧的圆心，轨道上方的A处有一个可视为质点的质量m＝1 kg的小物块，小物块由静止开始下落后恰好沿切线进入圆弧轨道．此后小物块将沿圆弧轨道下滑，已知AO连线与水平方向的夹角θ＝45°，在轨道末端C点紧靠一质量M＝3 kg的长木板，木板上表面与圆弧轨道末端的切线相平，木板下表面与水平地面之间光滑，小物块与长木板间的动摩擦因数μ＝0.3，g取10 m/s2.求：
(1)小物块刚到达C点时的速度大小；
(2)小物块刚要到达圆弧轨道末端C点时对轨道的压力；
(3)要使小物块不滑出长木板，木板长度L至少为多少？
参考答案：（1）4
?m/s?（2）50N，方向竖直向下?（3）4m
本题解析：(1)小物块从A到C，根据机械能守恒有：
mg×2R＝
mv
，解得vC＝4?m/s.
(2)小物块刚要到C点，由牛顿第二定律有：
FN－mg＝mv/R，解得FN＝50 N.
由牛顿第三定律，小物块对C点的压力FN′＝50 N，方向竖直向下．
(3)设小物块刚滑到木板右端时达到共同速度，大小为v，小物块在长木板上滑行过程中，小物块与长木板的加速度分别为：am＝μmg/m，aM＝μmg/M
v＝vC－amt
v＝aMt
由能量守恒定律得：－μmgL＝?(M＋m)v2－mv
联立解得： L＝4 m.
本题难度：一般