时间:2017-11-05 16:46:28
1、简答题 在验证牛顿第二定律的实验中，某同学用控制变量法分别研究小车的加速度a与小车所受的合外力F的关系，及小车的加速度a与小车质量m的关系，并作出a-F图线和a-
| 1 m |
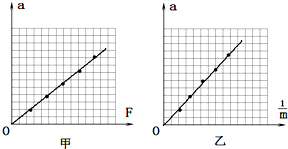
参考答案：a-F图象是过原点的倾斜直线，可以看出：a与F成正比；
a-1m图象也是过原点的倾斜直线，则a与1m成正比，即：物体的加速度与质量成反比
故答案为：正；反；
本题解析：
本题难度：一般
2、简答题 如图所示，质量为m=5kg的物体放在光滑水平面上，物体受到与水平面成θ=37°斜向上的拉力F=50N作用，由A点处静止开始运动，到B点时撤去拉力F，共经时间t=10s到达C点，已知AC间距离为L=144m，求：（sin37°=0.6，cos37°=0.8）
（1）物体在拉力F作用下运动的加速度a的大小；
（2）物体运动的最大速度vm的大小及拉力F作用的时间t1．
参考答案：（1）由牛顿第二定律Fcosθ=ma，
得a=8m/s2，
（2）它先加速后匀速，
则有：最大速度vm=at1，
而L=12vmt1+vm（t-t1），
得vm=16m/s，t1=2s
答：（1）物体在拉力F作用下运动的加速度a的大小为8m/s2；
（2）物体运动的最大速度vm的大小为16m/s，拉力F作用的时间为2s．
本题解析：
本题难度：一般
3、计算题 ．水平直轨道上运动的火车车厢内有一个倾角为37°的光滑斜面，斜面上有一个质量为m ="0.5" kg的小球，用轻绳系于斜面的顶端，如图12所示。在下列情况下，分别求出绳子的拉力大小和斜面对小球的支持力的大小。（sin37°=0.6，cos37°=0.8）
（1）火车以加速度a="8" m/s2向右加速运动；
（2）火车以加速度a=15m/s2向右加速运动；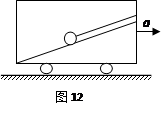
参考答案：
当球对斜面的压力刚好为零时，小球的受两个力，合力为水平向右（如图19-a所示）。
?，
则
?
（1）
，所以此时小球没有离开斜面，小球受三个力作用（如图19-b所示）而做匀加速运动，由正交分解得：
代入数据得T1=6.2N，? N1="1.6N?" 即拉力约6.2N、支持力约1.6N
（2）
，所以此时小球已离开斜面，小球受2个力作用，合力水平向右（如图19-c所示）。此时N2="0" ，
即拉力约9N、支持力为0
本题解析：略
本题难度：简单
4、选择题 如图倾角为30°的斜面体固定在水平地面上，一根不可伸长的轻绳两端分别系着小球A和物块B，跨过固定于斜面体顶端的滑轮O（可视为质点）,A的质量为m，B的质量为4m，开始时，用手托住A，使OA段绳恰处于水平伸直状态（绳中无拉力），OB绳平行于斜面，此时B静止不动，将A由静止释放，在其下摆过程中B始终保持静止，则在绳子到达竖直位置之前，下列说法正确的是（?）
A．物块B受到的摩擦力一直沿着斜面向上
B．物块B受到的摩擦力增大
C．绳子的张力先增大后减小
D．地面对斜面体的摩擦力方向一直水平向右
参考答案：D
本题解析：初始情况下分析物块B受力：竖直向下的重力
、垂直斜面向上的支持力
、沿斜面向上的静摩擦力Ff．沿斜面和垂直斜面正交分解B物块受到的力，故B物块处于平衡状态，则有：沿斜面方向：
，垂直斜面方向
，由牛顿第三定律知：物块B对斜面有垂直斜面向下的压力
和沿斜面向下的静摩擦力
，把这两个力向水平方向分解，则得：斜面体水平方向受到B的作用力（取水平向左为正方向）：
，又因为
，
，所以
，所以初始状态下斜面体水平方向受物块B的合力为零，不存在受地面的摩擦力．小球A下摆过程中，物块B始终保持静止，则小球A不对外做功，机械能守恒，小球A的速度不断增大，到最低点时速度最大，这时小球A摆到低时对绳的拉力最大，设r为A到滑轮的绳长，最低点小球A的速度为v，则由机械能守恒定律得：
，又由牛顿第二定律得：
，所以小球A对绳的拉力为
，此时物块B在平行于斜面方向所受的摩擦力
，方向沿斜面向下，由此可知物块B受到斜面的摩擦力先是沿斜面向上2mg，后逐渐减少到零，再沿斜面向下逐渐增大到mg，AB错误，
由以上分析知绳子的张力一直增大，小球A摆到低时对绳的拉力最大，所以，选项C错误．将A由静止释放，在其下摆过程中B始终保持静止，在绳子到达竖直位置之前，把斜面与物块B看做整体，绳子始终有拉力，此拉力水平向左有个分力，而整体保持静止，水平方向受力平衡，因此，地面对斜面体的摩擦力方向一直水平向右，那么，选项D正确．
考点：
点评：本题解答时要正确的分析好物体的受力，同时，要选好受力的研究对象：分析绳子拉力时选小球A，分析物块B受的摩擦力时选B物块，分析地面的摩擦力时选斜面与B物块整体，再者要注意物块B所受到的摩擦力是否达到最大值．
本题难度：一般
5、简答题 在电梯上一个质量为m的人，站在电子秤上．电梯运动过程中电子秤的示数分别如图甲、乙、丙所示．其中甲、乙、丙三图分别是匀加速运动、匀速直线运动、匀减速直线运动时体重计的示数（g取10m/s2）．请计算：
（1）人的质量m；
（2）电梯在变速运动过程中的加速度分别是多大．
参考答案：（1）由于乙图秤的示数F=600N，
由牛顿第三定律可得秤对人的支持力为F′=600N
又因为匀速运动所以F′=mg=600N所以人的质量?m=60kg
（2）对于甲图是匀加速过程中秤的示数F1=720N
由牛顿第三定律可得秤对人的支持力为F1′=720N．
由牛顿第二定律的?F1′-mg=ma
加速度a=2m/s2
对于丙图是匀减速过程中秤的示数F2=480N
由牛顿第三定律可得秤对人的支持力为F2′=480N．
由牛顿第二定律的?mg-F2′=ma
加速度大小a=2m/s2
答：（1）人的质量为60kg；（2）电梯在变甲图中的加速度小大为2m/s2，在丙图中的加速度大小为2m/s2．
本题解析：
本题难度：一般