时间:2017-11-05 16:41:30
1、计算题 （18分）如图所示，一质量为m的小物块B，放在质量为M的长木板A的左端，m=3M。长木板A静止在光滑水平面上，A、B之间的动摩擦因数为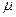
。现使二者一起以初速度
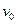开始向右运动，运动一段距离后，长木板A与固定竖直挡板相撞。已知A与挡板碰撞时间极短，且无机械能损失。运动过程中，B始终没从长木板A上脱落。求：
（1）长木板A第二次与挡板碰撞前，B在A上的滑痕长度s；
（2）当长木板A长度L满足什么条件时，保证B不会从A上脱落。
参考答案：（1）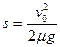
（2）
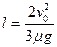
本题解析：（1）长木板A与挡板碰后，被等速率反弹。木板A与物B系统动量守恒，设第一次达到共速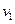
，取向左为正。则有：
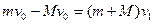…………4分
解得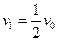
方向向右…………（2分）
长木板A向左作匀减速运动，共速时滑痕最长。设最大滑痕为s1
据能量守恒：
?
……………（4分）
解得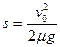：…………（2分）
（2）B始终没从板A上脱落，则长木板A与B将再次共速，一起向右运动，重复（1）问中的运动，直至二者速度均为零，板A右端挨着挡板。由于B一直相对A向右运
动，则B相对A滑动的总路程与B相对A滑动的位移相等。设木板最短长度为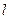
，据系统能量守恒则有：
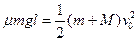…………（4分）
解得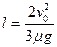：…………（2分）
本题难度：简单
2、选择题 如图所示，质量分别为m和2m的A、B两物块用轻弹簧相连，放在光滑水平面上，A靠紧竖直墙。现用力F向左缓慢推物块B压缩弹簧，当力F做功为W时，突然撤去F，在A物体开始运动以后，弹簧弹性势能的最大值是( )
A.W/3 B.W/2 C.2W/3 D.W
参考答案：A
本题解析：由题意知，当B向右运动至弹簧恢复原长时A开始运动，此时B的速度为v0，根据能量守恒可得：
，当A、B速度相等时，弹簧弹性势能最大，再根据动量守恒可得：2mv0=3mv，再根据能量守恒可知此时弹性势能
，解得：EP=W/3
考点：本题考查能量守恒、动量守恒
本题难度：一般
3、简答题 
(2)若两小球恰从下边界上的O′点离开电场，则金属板长度L应为多长？并在图示坐标纸上画出两小球在电场中水平方向和竖直方向两个分运动的v-t图象，要求标明坐标值。
参考答案：（1）两小球不能与M板发生碰撞
（2）
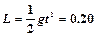m
本题解析：(1)小球B滑到最低点时的速度为v0，由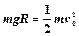
? (2分)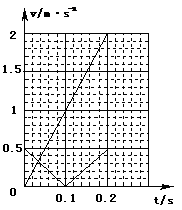
得v0=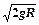
="1m/s?" (1分)
两小球碰后的共同速度设为v1，由动量守恒定律得
? (2分)
解得v1="0.5m/s?" ? (1分)
碰后两小球进入匀强电场，水平方向做匀减速直线运动，竖直方向做自由落体运动
水平方向上加速度大小为：
m/s2? (2分)
当水平分速度减为零时，向左运动的位移最大，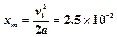
m? (2分)
因为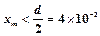
m? (1分)
故两小球不能与M板发生碰撞。? (1分)
(2)两小球恰从O′点离开电场，则两小球在电场中运动的时间为
s? (1分)
得金属板长度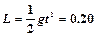m? (2分)
两个分运动的v-t图象如图所示。? (3分)
本题难度：一般
4、选择题 在质量为M的小车中悬挂一单摆，摆球的质量为m0，小车和单摆以恒定的速度V沿光滑水平地面运动，与位于正对面的质量为m的静止木块发生碰撞，碰撞时间极短，在此碰撞过程中，下列哪些情况可能发生
A．小车、木块、摆球的速度均发生变化，分别变为V1、V2、V3，满足（M+m0）V＝MV1+m V2+m0V3
B．摆球的速度不变，小车和木块的速度变为V1和V2，满足MV＝MV1+m V2
C．摆球的速度不变，小车和木块的速度变为V`，满足MV＝（M+m）V`
D．小车和摆球的速度均变为V1，木块的速度变为V2，满足（M+m0）V＝（M+m0）V1+mV2
参考答案：BC
本题解析：碰撞的瞬间小车和木块组成的系统动量守恒，摆球的速度在瞬间不变，以球的初速度方向为正方向，若碰后小车和木块的速度变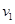
和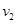
，由动量守恒定律得：
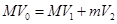；若碰后小车和木块速度相同，由动量守恒定律得：
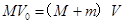，故BC正确。
考点：考查了动量守恒定律的应用
本题难度：一般
5、选择题 质量相等的A、B两球在光滑水平面上沿同一直线运动，A球的动量是7kg·m/s，B球的动量是3kg·m/s，当A球追上B球时发生碰撞，则碰撞后A、B两球的动量可能值是
A．PA=5kg·m/s，PB= 5kg·m/s? B．PA=6kg·m/s，PB=4kg·m/s
C．PA=-2kg·m/s，PB=12kg·m/s? D．PA=-4kg·m/s，PB=17kg·m/s
参考答案：A
本题解析：本题考查的是动量守恒定律等问题，两球相碰满足动量守恒，如果开始是同向运动，两球质量相等，则碰后动量相等，A选项符合实际情况，如果开始是反向运动，两球质量相等，则碰后动量仍然相等，都是2kg·m/s，故只有A选项正确；
本题难度：一般