时间:2017-11-05 16:41:30
1、选择题 质量为m的小球A在光滑的水平面上以速度v与静止在光滑水平面上的质量为2m的小球B发生正碰,碰撞后,A球的动能变为原来的1/9,那么碰撞后B球的速度夫小可能是
A.
B.
C.
D.
参考答案:AB
本题解析:分析:碰后A球的动能恰好变为原来的 ,速度大小变为原来的
,速度大小变为原来的 ,但速度方向可能跟原来相同,也可能相反,再根据碰撞过程中动量守恒即可解题.
,但速度方向可能跟原来相同,也可能相反,再根据碰撞过程中动量守恒即可解题.
解答:解:根据碰后A球的动能恰好变为原来的 ,得:
,得: mv2=
mv2= ?
? mv02
mv02
v=± ,碰撞过程中AB动量守恒,则mv0=mv+2mvB
,碰撞过程中AB动量守恒,则mv0=mv+2mvB
解得:vB= 或vB=
或vB=
故选AB.
点评:本题考查的是动量定律得直接应用,注意动能是标量,速度是矢量,难度适中,属于中档题.
本题难度:简单
2、填空题 光滑水平面上停着一辆长为L的平板车,车的一端放着质量为m的木箱,车的另一端站着质量为3m的人,车的质量为5m,若人沿车面走到木箱处将木箱搬放到车的正中央,则在这段时间内,车的位移大小为______.
参考答案:人从车的一端走到另一端时,设车的位移为x1,则人的位移为L-x1,
由动量守恒定律得:3mL-x1t1-(m+5m)x1t1=0,解得:x1=L3;
人搬着箱子走到车正中央时,设车的位移为x2,则人的位移为12L-x2,
由动量守恒定律得:(3m+m)12L-x2t2-5mx2t2=0,解得:x2=2L9,
整个过程,车的位移x=x1-x2=L3-2L9=L9;
故答案为:L9.
本题解析:
本题难度:一般
3、实验题 “验证动量守恒定律”(装置如图所示)。
(1)为了避免碰撞后入射的小球反弹到斜槽上而引起系统误差,入射小球的质量m1与被撞小球的质量m2的关系是m1_________(填“大”、“小”或“等”)于m2(两小球大小相等,直径已量出为d)。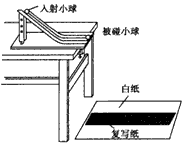
(2)为了保证入射小球水平抛出,必须调整斜槽,使_________。
(3)现提供以下实验步骤:
A.确定铅锤对应点O
B.不放m2,让m1从斜槽滚下,确定它落地点的位置P (地上有复写纸、白纸)
C.放m2于立柱上,让m1从斜槽滚下,与m2正碰后,确定m1、m2落地点的位置M、N
D.量OM,OP,ON
E.看m1OM+m2ON与m1OP是否相等,以验证动量守恒定律
指出上述步骤的不完善之处:答:___________________________
参考答案:(1)大
(2)出口水平
(3)B、C两步骤应是:让m1从同一位置由静止释放,重复10次,……确定,m1(m2)落地点的平均位置;E步骤应是:看
本题解析:
本题难度:一般
4、计算题 如图所示,倾斜轨道AB的倾角为37o,CD、EF轨道水平,AB与CD通过光滑圆弧管道BC连接,CD右端与竖直光滑圆周轨道相连。小球可以从D进入该轨道,沿轨道内侧运动,从E滑出该轨道进入EF水平轨道。a、b为两完全相同的小球,a球由静止从A点释放,在C处与b球发生弹性碰撞。已知AB长为5R,CD长为R,重力加速度为g,小球与斜轨AB及水平轨道CD、EF的动摩擦因数均为0.5,sin37o=0.6,cos37o=0.8,圆弧管道BC入口B与出口C的高度差为1.8R。求: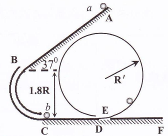
⑴a球滑到斜面底端C时速度为多大?a、b球在C处碰后速度各为多少?
⑵要使小球在运动过程中不脱离轨道,竖直圆周轨道的半径R′应该满足什么条件?若R′=2.5R,两球最后所停位置距D(或E)多远?
注:在运算中,根号中的数值无需算出。
参考答案:⑴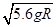 ?;
?;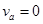 ?,
?,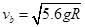 ?⑵
?⑵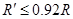 或
或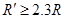 ;b球将停在D点左侧,距D点0.6R处, a球停在D点左侧,距D点R处。
;b球将停在D点左侧,距D点0.6R处, a球停在D点左侧,距D点R处。
本题解析:(1)设a球到达C点时速度为v,a球从A运动至C过程,由动能定理有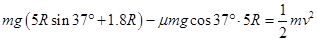 ?①
?①
可得?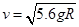 ?②
?②
b球在C发生弹性碰撞,系统动量守恒,机械能守恒,设a、b碰后瞬间速度分别为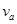 、
、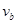 ,则有
,则有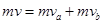 ③
③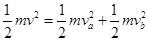 ④
④
由②③④可得?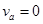 ?
?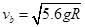 ?⑤
?⑤
可知,a、b碰后交换速度,a静止,b向右运动。
(2)要使小球b不脱离轨道,有两种情况:
情况一:小球b能滑过圆周轨道最高点,进入EF轨道。则小球b在最高点P应满足?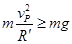 ?⑥
?⑥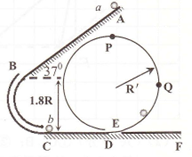
小球b碰后直到P点过程,由动能定理,有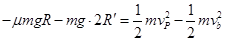 ?⑦
?⑦
由⑤⑥⑦式,可得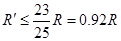 ?
?
情况二:小球b上滑至四分之一圆轨道的Q点时,速度减为零,然后滑回D。则由动能定理有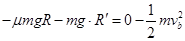 ?⑧
?⑧
由⑤⑧式,可得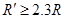 ?
?
若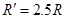 ,由上面分析可知,b球必定滑回D,设其能向左滑过DC轨道与a球碰撞,且a球到达B点,在B点的速度为
,由上面分析可知,b球必定滑回D,设其能向左滑过DC轨道与a球碰撞,且a球到达B点,在B点的速度为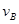 ,,由于a、b碰撞无能量损失,则由能量守恒定律有?
,,由于a、b碰撞无能量损失,则由能量守恒定律有?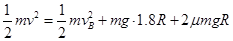 ?⑨
?⑨
由⑤⑨式,可得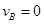 ?
?
故知,a球不能滑回倾斜轨道AB,a、b两球将在A、Q之间做往返运动,最终a球将停在C处,b球将停在CD轨道上的某处。设b球在CD轨道上运动的总路程为S,由于a、b碰撞无能量损失,则由能量守恒定律,有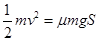 ?⑩
?⑩
由⑤⑩两式,可得? S=5.6R
所以知,b球将停在D点左侧,距D点0.6R处, a球停在D点左侧,距D点R处。
点评:弹性碰撞一般要用动量守恒和碰撞前后动能不变列表达式求解,本题中还要注意小球不脱离轨道有两种情况,其中上升到与圆心等高速度减小为零的情况容易忽视。
本题难度:一般
5、选择题 如图,长为a的轻质细线,一端悬挂在O点,另一端接一个质量为m的小球(可视为质点),组成一个能绕O点在竖直面内自由转动的振子.现有3个这样的振子,以相等的间隔b(b>2a)在同一竖直面里成一直线悬于光滑的平台MN上,悬点距台面高均为a.今有一质量为3m的小球以水平速度v沿台面射向振子并与振子依次发生弹性正碰,为使每个振子碰撞后都能在竖直面内至少做一个完整的圆周运动,则入射小球的速度v不能小于(? )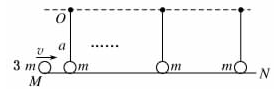
A.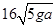
B.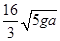
C.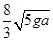
D.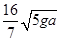
参考答案:C
本题解析:3m和m弹性碰撞:3mv=3mv′+mv1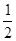 ×3mv2=
×3mv2=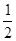 ×3mv′2+
×3mv′2+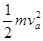 ,得v′=
,得v′=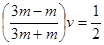
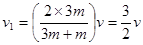
同理3m与第二个m弹性碰撞后得v″=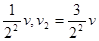
3m与第三个球碰后得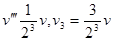
所以va>vb>vc,只要第三个球能做完整的圆周运动,则前两球一定能做完整的圆周运动.第三个球碰后,由机械能守恒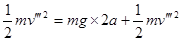 而
而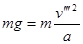 ,解之得
,解之得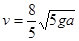 故C正确,故选C
故C正确,故选C
点评:本题难度较小,应用动量守恒定律求解问题时,首先应明确研究系统,判断初末状态动量
本题难度:一般