时间:2017-11-05 16:12:25
1、选择题 三个速度大小不同的的同种带电粒子，沿如图所示长方形区域匀强磁场的上边缘射入，当它们从下边缘飞出时，对入射方向的偏角分别为900、600、300，则它们在磁场中运动时间之比为?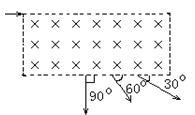
A．1：1：1
B．1：2：3
C．3：2：1
D．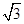
：
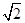：1
参考答案：C
本题解析：根据速度的偏转角等于粒子轨迹所对的圆心角，又因为是同一种粒子所以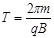
相同，圆心之比即为运动时间之比3：2：1 ，C对。
本题难度：简单
2、选择题 如图所示，在空间中取正交坐标系Oxyz（仅画出正半轴），沿x轴有一无限长通电直导线，电流沿x轴正方向，一束电子（重力不计）沿y=0，z=2的直线上（图中虚线所示）作匀速直线运动，方向也向x轴正方向，下列分析可以使电子完成以上运动的是
[? ]
A．空间另有且仅有沿Z轴正向的匀强电场
B．空间另有且仅有沿Z轴负向的匀强电场
C．空间另有且仅有沿y轴正向的匀强磁场
D．空间另有且仅有沿y轴负向的匀强磁场
参考答案：AC
本题解析：
本题难度：一般
3、计算题 图中MN表示真空室中垂直于纸面的平板，它的一侧有匀强磁场，磁场方向垂直于纸面向里，磁感应强度大小为B。一带电粒子从平板上狭缝O处以垂直于平板的初速v射入磁场区域，最后到达平板上的P点。已知B、v以及P到O的距离L，不计重力，求此粒子的电荷e与质量m之比。
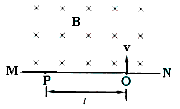
参考答案：解：粒子初速v垂直于磁场，粒子在磁场中受洛伦兹力而做匀速圆周运动
设其半径为R，由洛伦兹力公式和牛顿第二定律，有：
因为：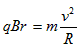
①
因粒子经O点时的速度垂直于OP，故OP是直径：L=2R ②
由此得：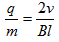
③
本题解析：
本题难度：一般
4、选择题 如图所示，在x轴上方存在垂直于纸面向里的匀强磁场，磁感应强度为B．在xOy平面内，从原点O处沿与x轴正方向成θ角（0＜θ＜π）以速率v发射一个带正电的粒子（重力不计）．则下列说法正确的是（ ）
A．若θ一定，v越大，则粒子在磁场中运动的时间越短
B．若θ一定，v越大，则粒子在磁场中运动的角速度越大
C．若v一定，θ越大，则粒子在磁场中运动的时间越短
D．若v一定，θ越大，则粒子在离开磁场的位置距O点越远
参考答案：A、D如图，画出粒子在磁场中运动的轨迹．由几何关系得：轨迹对应的圆心角α=2π-2θ
粒子在磁场中运动的时间t=α2πT=2π-2θ2π?2πmqB=(2π-2θ)mqB
则得知：粒子的运动时间与v无关，故A错误；
若v一定，θ越大，则粒子在磁场中运动的时间越短，故C正确；
B、粒子在磁场中运动的角速度ω=2πT，又T=2πmqB，则得ω=qBm，与速度v无关．故B错误．
D、设粒子的轨迹半径为r，则r=mvqB．如图，AO=2rsinθ=2mvsinθqB，则若θ是锐角，θ越大，AO越大．若θ是钝角，θ越大，AO越小．故D错误．
故选：C．
本题解析：
本题难度：简单
5、选择题 一个带电粒子处于垂直于匀强磁场方向的平面内，在磁场力的作用下做圆周运动．要想确定带电粒子的电荷量与质量之比，则需知道（ ）
A．运动速度v和磁感应强度B
B．轨道半径R和磁感应强度B
C．轨道半径R和运动速度v
D．磁感应强度B和运动周期T
参考答案：根据洛伦兹力做为向心力，可得，
qvB=mv2r=mr4π2T2，
所以比荷qm=v?rB，
所以要确定带电粒子的电荷量与质量之比，需要知道v，r和B．
根据T=2πmqB可得，
比荷qm=2πTB，
所以要确定带电粒子的电荷量与质量之比，需要知道磁感应强度B和运动周期T，所以D正确．
故选D．
本题解析：
本题难度：一般