时间:2017-09-26 11:40:09
1、选择题 某空间存在着如图甲所示足够大沿水平方向的匀强磁场。在磁场中A、B两个物块叠放在一起，置于光滑水平面上，物块A带正电，物块B不带电且表面绝缘。在t1=0时刻，水平恒力F作用在物块B上，物块A、B由静止开始做加速度相同的运动．在A、B一起向左运动的过程中，以下说法正确的是(? )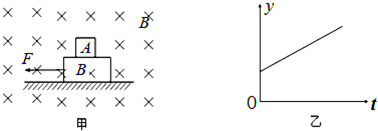 
A．图乙可以反映A所受洛仑兹力大小随时间t变化的关系
B．图乙可以反映A对B的摩擦力大小随时间t变化的关系
C．图乙可以反映A对B的压力大小随时间t变化的关系
D．图乙可以反映B对地面压力大小随时间t变化的关系
参考答案：CD
本题解析：以AB整体为研究对象，进行受力分析可知，竖直方向上受力平衡，整体所受合外力为F，由牛顿第二定律可知，整体做匀加速直线运动，故有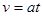
，A物体所受的洛伦兹力
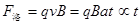，所以其
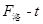图像应该是一条过原点的直线，故A错误；以A物体为研究对象有
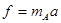，可知AB间的静摩擦力为定值，所以B选项错误；A对B的压力等于B对A的支持力，
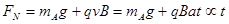，故C正确；同理，B对地面的压力等于地面对B的支持力，正比于时间t，故D正确。
本题难度：一般
2、简答题 如图所示，匀强电场方向水平向右，匀强磁场方向垂直纸面向里，质量为m，带电量为?q的粒子以速度v与磁场垂直，与电场成45°角射入恰能做匀速直线运动（重力加速度为g）．求：磁感应强度B的大小．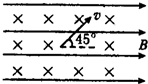
参考答案：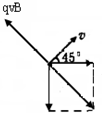
假设粒子不带正电，则所受电场力方向水平向左，洛伦兹力方向斜向右下方与v垂直，可以从力的平衡条件判断出这样的粒子不可能做匀速直线运动，所以粒子应带正电荷，受力情况如图所示，根据合外力为零得：
qvBcos45°=mg
∴B=
本题解析：
本题难度：一般
3、简答题 如图甲是一种自由电子激光器的原理示意图。经电场加速后的高速电子束，射入上下排列着许多磁铁的管中。相邻两块磁铁的极性是相反的。电子在垂直于磁场的方向上摆动着前进，电子在摆动的过程中发射出光子。管子两端的反射镜（图中未画出）使光子来回反射，光子与自由电子发生相互作用，使光子能量不断增大，从而产生激光输出。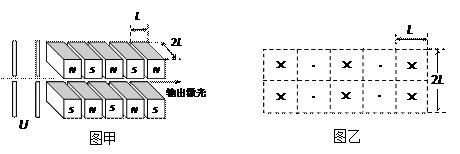
（1）若该激光器发射激光的功率为P = 6.63×10 9 W，激光的频率为υ = 1.0×1016 Hz。则该激光器每秒发出多少个激光光子？（普朗克常量
= 6.63×10－34 J·s）
（2）若加速电压U =1.8×10 4 V，取电子质量
= 9×10－31 kg，电子电荷量e =1.6×10－19C。每对磁极间的磁场可看作匀强磁场，磁感应强度为B = 9×10－4 T。每个磁极的左右宽度为L="30" cm，厚度为2 L 。忽略左右磁极间的缝隙距离，认为电子在磁场中运动的速度大小不变。电子经电场加速后，从上下磁极间缝隙的正中间垂直于磁场方向射入第1对磁极的磁场中，电子一共可通过几对磁极？在图乙的俯视图中，画出电子在磁场中运动轨迹的示意图（尺寸比图甲略有放大）。
?
参考答案：（1）?1.0×10 27?（2）3
本题解析：（1）每个激光光子的能量?E = hυ?（3分）
设激光器每秒发射n个光子?Pt = (nt) E （3分）
求出 ?n = 1.0×10 27?（1分）
（2）设电子经电场加速获得的速度为v
由动能定理?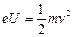
（2分）
设电子在磁场中做圆周运动的轨道半径为R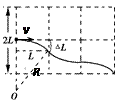
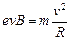?（2分）
电子在磁极间的运动轨迹如右图所示 （4分）
（只画出第一段圆弧，若比例对给2分，比例不对不给分。）
电子穿过每对磁极的侧移距离均相同，设为ΔL
由图可知 ΔL = R－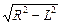
?（2分）(=0.1m)
电子通过的磁极个数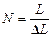 
? （2分）(=
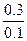=3)
求出 ? N =" 3" ? （1分）
本题难度：一般
4、计算题 如图所示，坐标系xOy在竖直平面内，水平轨道AB和斜面BC均光滑且绝缘，AB和BC的长度均为L，斜面BC与水平地面间的夹角θ=60°，有一质量为m、电量为+q的带电小球（可看成质点）被放在A点。已知在第一象限分布着互相垂直的匀强电场和匀强磁场，电场方向竖直向上，场强大小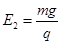
，磁场垂直纸面向外，磁感应强度大小为B；在第二象限分布着沿x轴正向的匀强电场，场强大小未知。现将放在A点的带电小球由静止释放，恰能到达C点，问
（1）分析说明小球在第一象限做什么运动；
（2）小球运动到B点的速度；
（3）第二象限内匀强电场的场强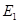
；
参考答案：（1）匀速圆周运动，（2）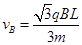
，（3）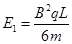
。
本题解析：（1）当带电小球进入第一象限后所受电场力为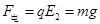
，即带电小球所受电场力与所受重力相平衡，小球所受合外力为洛伦兹力始终垂直与速度方向，故小球做匀速圆周运动；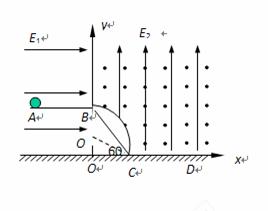
（2）有几何关系可得：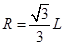
，又因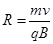
，故有小球在B点速度为；
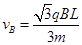（3）在加速电场中，A到B过程使用动能定律：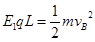
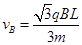，代入 ，可得。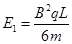
考点：本题考查了带电电荷在电磁场中的运动
本题难度：一般
5、计算题 如图所示，相距为R的两块平行金属板M，N正对着放置，S1，S2分别为M，N板上的小孔，S1，S2，O三点共线，它们的连线垂直M，N，且S2O=R。以O为圆心、R为半径的圆形区域内存在磁感应强度为B、方向垂直纸面向外的匀强磁场。D为收集板，板上各点到O点的距离以及板两端点的距离都为2R，板两端 点的连线垂直M，N板。质量为m、带电量为+q的粒子，经S1进入M，N间的电场后，通过S2进入磁场，粒子在S1处的速度和粒子所受的重力均不计。
(1)当M，N间的电压为U时，求粒子进入磁场时速度的大小v；
(2)若粒子恰好打在收集板D的中点上，求M，N间的电压值U0；
(3)当M，N间的电压不同时，粒子从S1到打在D上经历的时间t会不同，求t的最小值。
参考答案：解：(1)粒子从S1到达S2的过程中，根据动能定理得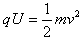
①
解得粒子进入磁场时速度的大小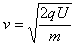
(2)粒子进入磁场后在洛伦兹力作用下做匀速圆周运动有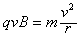
②
由①②得加速电压U与轨迹半径r的关系为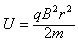
当粒子打在收集板D的中点时，粒子在磁场中运动的半径r0=R
对应电压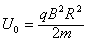
(3)M，N间的电压越大，粒子进入磁场时的速度越大，粒子在极板间经历的时间越短，同时在磁场中运动轨迹的半径越大，在磁场中运动的时间也会越短，出磁场后匀速运动的时间也越短，所以当粒子打在收集板D的右端时，对应时间t最短
根据几何关系可以求得粒子在磁场中运动的半径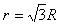
由②得粒子进入磁场时速度的大小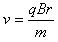
粒子在电场中经历的时间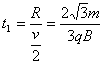
粒子在磁场中经历的时间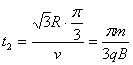
粒子出磁场后做匀速直线运动经历的时间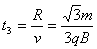
粒子从S1到打在收集板D上经历的最短时间为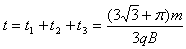
本题解析：
本题难度：困难