时间:2017-09-26 11:15:02
1、选择题 如图所示，通有恒定电流的直导线MN与闭合金属框共面，第一次将金属框由位置Ⅰ移动到位置Ⅱ，第二次将金属框由位置Ⅰ翻转到位置Ⅱ，设两次通过金属框截面的电量分别为q1和q2，则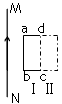 
[? ]
A．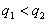
B．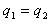
C．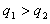
D．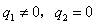
参考答案：A
本题解析：
本题难度：一般
2、简答题 如图（甲）所示，光滑的平行水平金属导轨MN、PQ相距l，在M点和P点间连接一个阻值为R的电阻，一质量为m、电阻为r、长度也刚好为l的导体棒垂直搁在导轨上a、b两点间，在a点右侧导轨间加一有界匀强磁场，磁场方向垂直于导轨平面，宽度为d0，磁感应强度为B，设磁场左边界到ab距离为d．现用一个水平向右的力F拉导体棒，使它从a、b处静止开始运动，棒离开磁场前已做匀速直线运动，与导轨始终保持良好接触，导轨电阻不计，水平力F-x的变化情况如图（乙）所示，F0已知．求：
（1）棒ab离开磁场右边界时的速度；
（2）棒ab通过磁场区域的过程中整个回路所消耗的电能E；
（3）d满足什么条件时，棒ab进入磁场后一直做匀速运动；
（4）若改变d的数值，定性画出棒ab从静止运动到d+d0的过程中v2-x的可能图线（棒离开磁场前已做匀速直线运动）．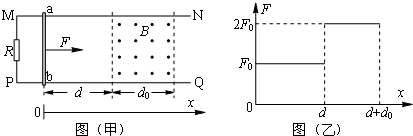
参考答案：
（1）设离开右边界时棒ab速度为v，
则有，感应电动势，E=BLv
闭合电路欧姆定律，I=ER+r?
对棒有?2F0-BIL=0?
解得：v=2F0(R+r)B2L2?
（2）在ab棒运动的整个过程中，根据动能定理：
F0d+2F0d0-W安=12mv2-0?
由功能关系：E电=W安?
解得：E电=F0(d+2d0)-2mF20(R+r)2B4L4?
（3）设棒刚进入磁场时的速度为v0，
则有F0d=12mv20?
当v0=v，即d=2F0m(r+R)2B4L4时，进入磁场后一直匀速运动?
（4）可能的图象如下图所示?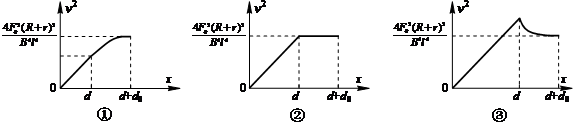
答：（1）棒ab离开磁场右边界时的速度为2F0(R+r)B2L2；
（2）棒ab通过磁场区域的过程中整个回路所消耗的电能为F0(d+2d0)-2mF20(R+r)2B4L4；
（3）当d=2F0m(r+R)2B4L4条件时，棒ab进入磁场后一直做匀速运动；
本题解析：
本题难度：一般
3、计算题 如图甲所示，水平面上有两电阻不计的光滑金属导轨平行固定放置，间距d=0．5m，导轨左端通过导线与阻值为2Ω的电阻R连接，右端通过导线与阻值为4Ω的小灯泡L连接。在矩形区域CDFE内有竖直向上的匀强磁场，CE长为2m，CDFE区域内磁场的磁感应强度B随时间变化的关系如图乙所示，在t=0时，一阻值为2Ω的金属棒在水平恒力F作用下由静止开始从AB位置沿导轨向右运动，在金属棒从AB位置运动到EF位置的过程中，小灯泡的亮度没有发生变化，求：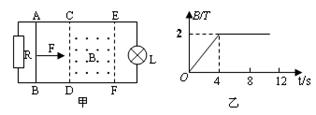
（1）通过小灯泡的电流大小?
（2）恒力F的大小?
（3）4s末金属棒的速度大小?
（4）金属棒的质量
参考答案：（1）0.1A?（2）0.3N?（3）1m/s?（4）1.2kg
本题解析：（1）金属棒未进入磁场时，
由法拉第电磁感应定律可得：
通过小灯泡的电流
（2）因灯泡亮度不变，故4s末金属棒恰好进入磁场且做匀速运动，此时金属棒中的电流为：
则恒力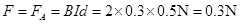
（3）4s后回路中的感应电动势为：
则可知4s末金属棒的速度
（4）由运动学公式可知前4s金属棒的加速度为：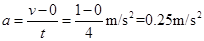
故金属棒的质量
点评：本题涉及到动生电动势和感生电动势，但二者却不是同时出现的，先是感生电动势，4s后是动生电动势，本题还要根据欧姆定律和串并联关系求解。
本题难度：一般
4、选择题 金属圆环的圆心为o，金属棒oa、ob与金属环接触良好且可绕o在环上转动，整个装置处于垂直纸面向里的匀强磁场中，如图所示，当外力使oa顺时针方向加速转动时，在oa追上ob之前，ob将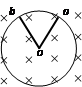
A．顺时针方向转动
B．逆时针方向转动
C．先顺时针方向转动，后逆时针方向转动
D．先逆时针方向转动，后顺时针方向转动
参考答案：A
本题解析：根据楞次定律，感应电流的磁通量总是阻碍引起感应电流的磁通量的变化，把aob和优弧ab构成的面积磁通量在增加，所以ob顺时针转动以阻止磁通量的增加，把aob和略
弧ab构成的平面磁通量在减少，所以ob顺时针方向转动以减少磁通量的减少，所以应选A
本题难度：简单
5、计算题 如图所示，两根正对的平行金属直轨道MN、M′N′位于同一水平面上，两轨道之间的距离l=0.50m．轨道的MM′端之间接一阻值R=0.40Ω的定值电阻，NN′端与两条位于竖直面内的半圆形光滑金属轨道NP、N′P′平滑连接，两半圆轨道的半径均为R0=0.50m．直轨道的右端处于竖直向下、磁感应强度B=0.64T的匀强磁场中，磁场区域的宽度d=0.80m，且其右边界与NN′重合．现有一质量m=0.20kg、电阻r=0.10Ω的导体杆ab静止在距磁场的左边界s=2.0m处．在与杆垂直的水平恒力F=2.0N的作用下ab杆开始运动，当运动至磁场的左边界时撤去F，结果导体ab恰好能以最小速度通过半圆形轨道的最高点PP′．已知导体杆ab在运动过程中与轨道接触良好，且始终与轨道垂直，导体杆ab与直轨道之间的动摩擦因数μ=0.10，轨道的电阻可忽略不计，取g=10m/s2，求： ?
（1）导体杆刚进入磁场时，通过导体杆上的电流大小和方向；
（2）导体杆穿过磁场的过程中通过电阻R上的电荷量；
（3）导体杆穿过磁场的过程中整个电路产生的焦耳热．?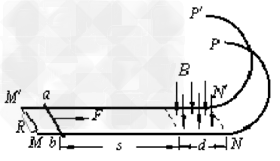 
参考答案：解：（1）设导体杆在F的作用下运动到磁场的左边界时的速度为υ1
根据动能定理则有（Fμmg）s=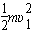
导体杆刚进入磁场时产生的感应电动势E=Blυ1
此时通过导体杆的电流大小I=E/（R+r）=3.8A（或3.84A）?
根据右手定则可知，电流方向为b向a
（2）设导体杆在磁场中运动的时间为t，产生的感应电动势的平均值为E平均
则由法拉第电磁感应定律有E平均=ΔΦ/t=Bld/t?
通过电阻R的感应电流的平均值为I平均=E平均/（R+r）
通过电阻R的电荷量q=I平均t=0.51C
（3）设导体杆离开磁场时的速度大小为υ2，运动到圆轨道最高点的速度为υ3，因导体杆恰好能以最小速度通过半圆形轨道的最高点，根据牛顿第二定律，对导体杆在轨道最高点时有?mg=mυ23/R0 ?
对于导体杆从NN′运动至PP′的过程，根据机械能守恒定律有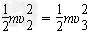
+mg2R0
解得υ2=5.0m/s
导体杆穿过磁场的过程中损失的机械能ΔE=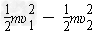
=1.1J
此过程中电路中产生的焦耳热为Q=ΔE－μmgd=0.94J
本题解析：
本题难度：困难