时间:2017-09-25 07:27:48
1、简答题 一艘宇宙飞船绕一个不知名的半径为R的行星表面飞行,环绕一周飞行时间为T,求该行星的质量和平均密度.
参考答案: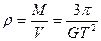 .
.
本题解析:本题考查应用万有引力定律处理实际问题的能力,以及构建理想化物理模型的能力.我们可以认为宇宙飞船围绕行星的中心做匀速圆周运动,其所需向心力由万有引力提供,飞船绕行星表面飞行,说明飞船运行的轨道半径约等于该行星的?半径.?
设宇宙飞船的质量为m,行星的质量为M,根据万有引力提供的向心力,则有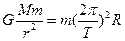 ,
,
该行星的体积为
所以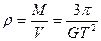 .
.
本题难度:简单
2、选择题 同步卫星周期为T1,加速度为a1,向心力为F1;地面附近的卫星的周期为T2,加速度为a2,向心力为F2,地球赤道上物体随地球自转的周期为T3,向心加速度为a3,向心力为F3,则( )
A.T1=T3≥T2
B.F1<F2=F3
C.a1<a2
D.a2<a3
参考答案:因为同步卫星和地球赤道上物体的周期相同,即T1=T3,根据a=r(2πT)2知,a1>a3.根据万有引力提供向心力得,GMmr2=ma=mr4π2T2,知轨道半径越大,向心加速度越小,周期越大,所以T1>T2,a1<a2.因为质量未知,故无法比较向心力的大小.故C正确,A、B、D错误.
故选C.
本题解析:
本题难度:简单
3、选择题 在低轨道运行的人造卫星,由于受到空气阻力的作用,卫星的轨道半径不断缩小,运行中卫星的( )
A.速率逐渐减小
B.速率逐渐增大
C.周期逐渐变小
D.向心力逐渐加大
参考答案:卫星在阻力的作用下,要在原来的轨道减速,万有引力将大于向心力,物体会做向心运动,轨道半径变小,人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r、地球质量为M,
AB、由GMmr2=mv2r
解得:v=
本题解析:
本题难度:简单
4、简答题 某行星的质量为M,半径为R,自转周期为T,已知万有引力常量为G,试求:
(1)该行星两极的重力加速度;
(2)该行星“赤道”上的重力加速度;
(3)要从该行星表面发射一颗质量为m0的“近地卫星”,至少应该补充多少机械能?
参考答案:(1)对于放置于行星两极的质量为m的物体,有万有引力等于重力得出:
GmMR2=mg?
得:g=GMR2
(2)对于放置于行星赤道上的质量为m的物体,它随行星做匀速圆周运动.设它受到的“地面”支持力为N,则有
GmMR2-N=ma?
其中a=4π2T2R?
N和重力是一对平衡力,所以N=mg′
解以上三式得g′=GMR2-4π2T2R?
(3)卫星在赤道上时,初速度最大,需要补充的机械能最少.
初速度v1=2πTR?
近地环绕时,有Gm0MR2=m0v22R
需要补充的机械能△E=12m0v22-12m0v21=2π2m0R2T2-GMm02R
答:(1)行星两极的重力加速度是GMR2;
(2)该行星“赤道”上的重力加速度是GMR2-4π2T2R;
(3)至少应该补充的机械能为2π2m0R2T2-GMm02R.
本题解析:
本题难度:一般
5、简答题 中国首个月球探测计划“嫦娥工程”预计在2017年送机器人上月球,实地采样送回地球,为载人登月及月球基地选址做准备.设想我国宇航员随“嫦娥”号登月飞船绕月球飞行,飞船上备有以下实验仪器:A.计时表一只;B.弹簧秤一把;C.已知质量为m的物体一个;D.天平一只(附砝码一盒).在飞船贴近月球表面时可近似看成绕月球做匀速圆周运动,宇航员测量出飞船在靠近月球表面的圆形轨道绕行N圈所用的时间为t.飞船的登月舱在月球上着陆后,遥控机器人利用所携带的仪器又进行了第二次测量,利用上述两次测量所得的物理量可出推导出月球的半径和质量.(已知万有引力常量为G)
(1)机器人进行第二次测量的内容是什么?
(2)试推导用上述测量的物理量表示的月球半径和质量的表达式.
参考答案:(1)机器人在月球上用弹簧秤竖直悬挂物体,静止时读出弹簧秤的读数F,即为物体在月球上所受重力的大小.?
(2)在月球上忽略月球的自转有?
F=GMmR2
对飞船靠近月球表面做圆周运动有?
GMmR2=m4π2T2R
又?T=tN
?由以上各式可得:
月球的半径R=Ft24π2N2m
月球的质量M=F3t416π4N4m3G
答:(1)机器人进行第二次测量的内容是测量物体在月球上所受的重力.
(2)月球的半径为R=Ft24π2N2m
?月球的质量为M=F3t416π4N4m3G
本题解析:
本题难度:一般