时间:2017-09-25 07:25:22
1、选择题 关于匀速圆周运动,以下说法不正确的是
[? ]
A.匀速圆周运动是变速运动
B.匀速圆周运动是变加速运动
C.向心加速度是描述线速度方向变化快慢的物理量
D.向心力的大小不变,方向总指向圆心,所以向心力为恒力
参考答案:D
本题解析:
本题难度:简单
2、选择题 有关圆周运动的基本模型,下列说法正确的是( )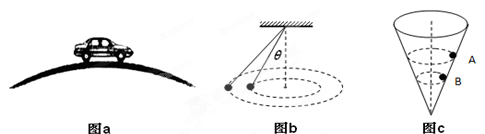
A.如图a,汽车通过拱桥的最高点处于超重状态
B.如图b所示是一圆锥摆,增大θ,但保持圆锥的高不变,则圆锥摆的角速度不变
C.如图c,同一小球在光滑而固定的圆锥筒内的A、B位置先后分别做匀速度圆周运动,则在A、B两位置小球的角速度及所受筒壁的支持力大小相等
D.火车转弯超过规定速度行驶时,内轨对内轮缘会有挤压作用
参考答案:B
本题解析:汽车通过拱桥的最高点时有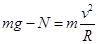 ,故得
,故得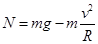 ,故处于失重状态,A错误;圆锥摆过程中重力和绳子的拉力充当向心力,故有
,故处于失重状态,A错误;圆锥摆过程中重力和绳子的拉力充当向心力,故有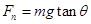 ,设圆锥的高度为h,则运动半径为
,设圆锥的高度为h,则运动半径为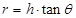 ,故有
,故有 ,解得
,解得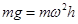 ,角速度大小与角度无关,B正确;在两个位置上小球的重力相同,支持力方向相同,所以合力相同,即向心力相同,根据公式
,角速度大小与角度无关,B正确;在两个位置上小球的重力相同,支持力方向相同,所以合力相同,即向心力相同,根据公式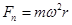 可得半径越大,角速度越小,故角速度不同,所受筒壁的支持力大小相等,故C错误;当火车在规定的速度转弯时,由支持力与重力的合力提供火车转弯所需的向心力.当速度大于规定的速度时,火车的支持力与重力的合力不足以来供火车转弯,就会出现侧翻现象,导致火车轮缘挤压外轨,故D错误;
可得半径越大,角速度越小,故角速度不同,所受筒壁的支持力大小相等,故C错误;当火车在规定的速度转弯时,由支持力与重力的合力提供火车转弯所需的向心力.当速度大于规定的速度时,火车的支持力与重力的合力不足以来供火车转弯,就会出现侧翻现象,导致火车轮缘挤压外轨,故D错误;
考点:考查了圆周运动实例分析
本题难度:一般
3、计算题 (16分)如图所示,用PM、QN是两根半径为d的光滑的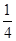 圆弧轨道,其间距为L,O、P连线水平,M.N在同一水平高度,圆弧轨道电阻不计,在其上端连有一阻值为R的电阻,整个装置处于竖直向上的匀强磁场中,磁感应强度大小为B。现有一根长度稍大于L、质量为m、电阻为m、电阻为r的金属棒从轨道的顶端P处由静止开始下滑,到达轨道底端MN时对轨道的压力为2mg,求:
圆弧轨道,其间距为L,O、P连线水平,M.N在同一水平高度,圆弧轨道电阻不计,在其上端连有一阻值为R的电阻,整个装置处于竖直向上的匀强磁场中,磁感应强度大小为B。现有一根长度稍大于L、质量为m、电阻为m、电阻为r的金属棒从轨道的顶端P处由静止开始下滑,到达轨道底端MN时对轨道的压力为2mg,求:
(1)棒到达最低点时金属棒两端的电压;
(2)棒下滑过程中金属棒产生的热量:
(3)棒下滑过程中通过金属棒的电量。
参考答案:(1)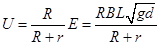 (2)
(2)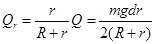 (3)
(3)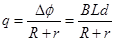
本题解析:(1)在轨道里的最低点MN处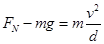 ?
?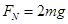
解得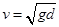
电动势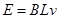
得:电压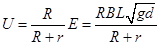
(2)由动能定理(能量守恒)得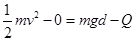
得金属棒产生的热量为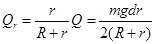
(3)电量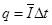 ,
,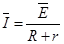 ,
,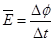
得到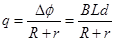
本题考查圆周运动和电磁感应现象,在最低点由合力提供向心力,可求得速度大小,由E=BLv可求得感应电动势,再由欧姆定律可求得路端电压大小,在金属棒运动过程中,重力势能转化为动能和焦耳热,串联电路中电流相等,结合焦耳热公式可知r和R的焦耳热分配与电阻成正比,由此可求得r上的焦耳热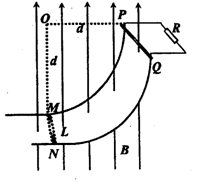
本题难度:一般
4、选择题 如图所示,一光滑圆环竖直放置,AB为其水平方向的直径,甲、乙两球以同样大小的初速度从A处出发,沿环内侧始终不脱离环运动到达B点,则( ) ?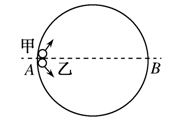
A.甲先到达B
B.乙先到达B
C.同时到达B
D.若质量相同,它们同时到达B
参考答案:B
本题解析:本题考查的是圆周运动的问题,圆环是光滑的,没有摩擦力的作用,在小球由A点开始运动的过程中,只有重力对小球做功,小球的机械能守恒,甲、乙两小球在A点的速度相同,又没有任何阻力做功,则小球在B点的速度大小也相等,且与A点的速度大小相等.甲小球是先减速后加速,而乙小球则是先加速后减速,到达B点的速度均相等,所以乙小球在运动的过程中的平均速度肯定要大于甲小球运动的平均速度,所以乙小球先到达,正确选项为B.
本题难度:一般
5、填空题 两颗人造卫星A、B绕地球做匀速圆周运动,它们的周期之比TA∶TB=1∶8,则其轨道半径之比是 运动速率之比是
参考答案:1:4 2:1
本题解析:分析:人造卫星绕地球做圆周运动受到的万有引力提供向心力,分别用周期、速率来表示向心力,化简公式即可求解结果.
解答:解:人造卫星绕地球做圆周运动受到的万有引力提供向心力,对A卫星有: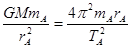 ,
,
对B卫星有: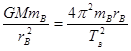 ,化简得:
,化简得: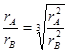 =
= 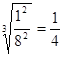 ;
;
用速度表示向心力,对A卫星有: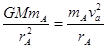 , 对B卫星有:
, 对B卫星有: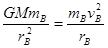 ,
,
化简得: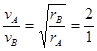 ,
,
故答案为:1:4,2:1.
点评:对于卫星问题一定掌握:万有引力提供向心力,可以用卫星的速度、周期、角速度来分别表示向心力,从而求出结果.
本题难度:一般