时间:2017-09-23 23:44:53
1、计算题 小球以15 m/s的水平初速度向一倾角为37°的斜面抛出,飞行一段时间后,恰好垂直撞在斜面上.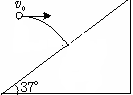
求:(1)小球在空中的飞行时间;(2)抛出点距落球点的高度.
(g="10" m/s2,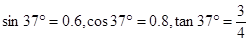 )
)
参考答案:(1)2s;(2)20m;
本题解析:将球垂直撞在斜面上的速度分解,如图所示.由图可知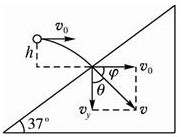
θ=37°,φ=90°-37°=53°……2分
tanφ=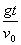 ,则t=
,则t= ·tanφ=
·tanφ=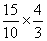 s="2" s……4分
s="2" s……4分
h=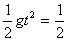 ×10×22 m="20" m.……4分
×10×22 m="20" m.……4分
点评:解决本题的关键知道垂直撞在斜面上,速度与斜面垂直,将速度分解为水平方向和竖直方向,根据水平分速度可以求出竖直分速度,从而可以求出运动的时间.
本题难度:简单
2、计算题 (10分)如图所示,一个小球从高h=10 m处以水平速度v0=10m/s抛出,撞在倾角θ=45°的斜面上的P点,已知AC=5 m,求: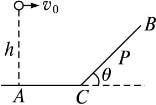
(1)P、C之间的距离;
(2)小球撞击P点时速度的大小和方向。
参考答案:(1)5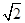 ?m?(2)10
?m?(2)10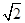 m/s? 45°
m/s? 45°
本题解析:(1)设P、C之间的距离为L,根据平抛运动规律,
5+Lcos 45°=v0t
h-Lsin 45°=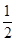 gt2,
gt2,
联立解得L=5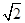 m,
m,
t=1s。
(2)小球撞击P点时的水平速度v=v0=10 m/s,竖直速度vy=gt=10m/s,
所以小球撞击P点时速度的大小为v=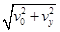 =10
=10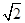 m/s,
m/s,
设小球的速度方向与水平方向的夹角为α,则tan α=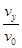 =1,α=45°,
=1,α=45°,
方向垂直于斜面向下,所以小球垂直于斜面向下撞击P点。
本题难度:一般
3、选择题 在某次自由式滑雪比赛中,一运动员从弧形雪坡上沿水平方向飞出后,又落回到斜面雪坡上,如图所示,若斜面雪坡的倾角为θ,飞出时的速度大小为v0,不计空气阻力,运动员飞出后在空中的姿势保持不变,重力加速度为g,则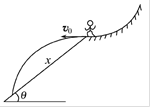
A.运动员在空中经历的时间是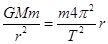
B.运动员落到雪坡时的速度大小是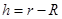
C.如果v0不同,则该运动员落到雪坡时的速度方向也就不同
D.不论v0多大,该运动员落到雪坡时的速度方向都是相同的
参考答案:D
本题解析:根据平抛运动的特点有,水平位移: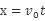 竖直位移:
竖直位移: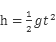
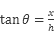 所以经历的时间:
所以经历的时间: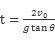 ,竖直方向的速度:
,竖直方向的速度: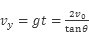 ,所以运动员落到雪坡时的速度大小是:
,所以运动员落到雪坡时的速度大小是: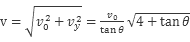 所以AB错;设运动员落到雪坡时的速度方向与水平面的夹角
所以AB错;设运动员落到雪坡时的速度方向与水平面的夹角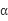 ,则有
,则有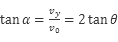 ,所以D正确。考点: 平抛运动
,所以D正确。考点: 平抛运动
本题难度:一般
4、选择题 对平抛物体运动,在下列哪些已知条件下可确定物体的初速度( )
A.只已知物体水平位移
B.已知物体下落的高度和重力加速度
C.已知物体位移大小和重力加速度
D.已知物体落地时速度大小和方向
参考答案:A、已知水平位移,由于不知道运动的时间,故无法求出物体的初速度.故A错误.
B、根据下落的高度和重力加速度,根据h=12gt2只能求出平抛运动的时间,由于水平位移未知,则无法求出平抛运动的初速度.故B错误.
C、已知位移的大小,由于位移的方向未知,则无法得知水平位移和竖直位移,不能求出初速度的大小.故C错误.
D、已知物体落地的速度大小和方向,根据平行四边形定则可以求出平抛运动的初速度.故D正确.
故选:D.
本题解析:
本题难度:简单
5、填空题 写出下列匀速圆周运动的公式,线速度的定义式v= ,角速度的定义式ω= 。平抛运动可分解为水平方向上的 运动和竖直方向上的 运动。
参考答案:rs/rt rφ/rt 匀速直线运动 自由落体运动
本题解析:匀速圆周运动的线速度的定义式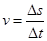 ;角速度的定义式
;角速度的定义式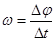 ;平抛运动可分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动。
;平抛运动可分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动。
考点:曲线运动的的基本公式和平抛运动的研究方法
点评:平时要牢记各个物理基本公式,熟练掌握一般问题的处理法方法。
本题难度:简单