时间:2017-09-23 23:37:13
1、计算题 如图所示，在倾角θ=37°的足够长的固定的斜面底端有一质量m=1.0 kg的物体，物体与斜面间动摩擦因数μ=0.25。现用轻细绳将物体由静止沿斜面向上拉动，拉力F=10.0 N，方向平行斜面向上。经时间t=4.0 s绳子突然断了，求：
（1）绳断时物体的速度大小。
（2）从绳子断了开始到物体再返回到斜面底端的运动时间。（sin37°=0.60，cos37°=0.80，g=10 m/s2）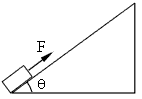 
参考答案：解：（1）物体受拉力向上加速运动过程，则有
F－mgsinθ－f=ma1
FN－mgcosθ=0
且f=μFN
由以上三式代数解得：a1=2.0 m/s2
所以t=4.0 s时物体的速度大小为v1=a1t=8.0 m/s
（2）绳断时物体距斜面底端的位移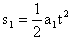
=16 m
绳断后物体沿斜面向上做匀减速直线运动，则有mgsinθ+μmgcosθ=ma2
解得a2=8.0 m/s2
物体做减速运动的时间t2=v1/a2=1.0 s
减速运动的位移s2=v1t2/2=4.0 m
此后物体将沿斜面匀加速下滑，则有mgsinθ－μmgcosθ=ma3
解得a3=4.0 m/s2
设物体由最高点到斜面底端的时间为t3，则有s1+s2=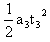
解得t3=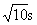
=3.2s
所以物体返回到斜面底端的时间为t总=t2+t3=4.2 s
本题解析：
本题难度：困难
2、计算题 如图所示，水平轨道PAB与圆弧轨道BC相切于B点，其中PA段光滑，AB段粗糙，动摩擦因数μ=0.1，AB段长度L=2m，BC段光滑，半径R=lm，轻质弹簧劲度系数k=200N/m，左端固定于P点，右端处于自由状态时位于A点。现用力推质量m=2kg的小滑块，使其缓慢压缩弹簧，当推力做功W=25J时撤去推力。已知弹簧弹性势能表达式，其中，k为弹篝的劲度系数，x为弹簧的形变量，重力加速度取g=10m/s2。
（1）求推力撤去瞬间，滑块的加速度a；
（2）求滑块第一次到达圆弧轨道最低点B时对B点的压力FN；
（3）判断滑块能否越过C点，如果能，求出滑块到达C点的速度vc和滑块离开C 点再次回到C点所用时间t，如果不能，求出滑块能达到的最大高度h。 
参考答案：解：（1）推力做功全部转化为弹簧的弹性势能，则有W=Ek①
则有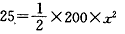
?
得x=0.5m②
由牛顿运动定律得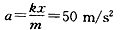
③
（2）设滑块到达B点时的速度为vB，由能量关系有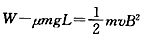
得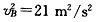
④
对滑块，由牛顿定律得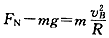
⑤
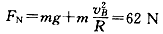⑥
由牛顿第三定律可知，滑块对B点的压力为62N⑦
（3）设滑块能够到达C点，且具有速度vC，由功能关系得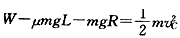
⑧
?代人数据解得vC=1m/s⑨
故滑块能够越过C点从滑块离开C点到再次回到C点过程中，
物体做匀变速运动，以向下为正方向，有vC=-vC十gt⑩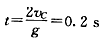 
本题解析：
本题难度：困难
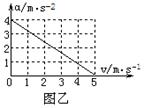
3、计算题 (12分)如图甲所示，一质量为m="1.0" kg的木块从倾角为α=37?、长度为L="3.2" m的固定粗糙斜面顶端由静止开始运动，同时木块受水平向左的风力作用，且水平风力与风速成正比，木块在斜面上下滑时的加速度a与风速v之间的关系如图乙所示。已知sin 37?=0.6，cos 37?=0.8，取重力加速度大小为g="10" m/s2，请求解：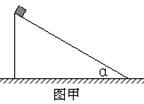
?
(1)木块与斜面间的动摩擦因数
(2)风速v="3.0" m/s时木块沿斜面下滑的时间t及木块所受水平风力F的大小。
参考答案：(1)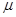
=0.25。(2) F=2.5N
本题解析：(1)当风速为0时，物体下滑的加速度为4.0m/s2，?（1分）
由牛顿定律得物体的加速度为：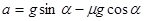
?（2分）
解得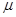：=0.25。?（1分）
(2) 由a-v图象可得：a=4-0.8v?（2分）
当v="3" m/s时，物体下滑的加速度为a=1.6m/s2?（1分）
由运动学公式得：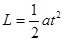
，解得：t=2.0s?（1分）
由牛顿第二定律得：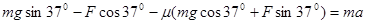
?（2分）
解得：F=2.5N?（2分）
点评：本题难度较小，对于力与运动的关系问题，可根据受力求解加速度再由牛顿第二定律求解，或现有牛顿第二定律求解加速度，再由运动学公式求解
本题难度：一般
4、选择题 如图，一光滑球靠在墙边静止，球受到的力有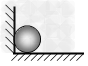
[? ]
A、1个?
B、2个?
C、3个?
D、4个
参考答案：B
本题解析：
本题难度：简单
5、选择题 下列关于加速度的说法，正确的是? (? )
A．物体的速度越大，加速度也就越大
B．物体的加速度为零，速度也一定为零
C．物体的加速度大小等于速度的变化量与时间的比值
D．物体的加速度的方向和速度变化的方向总是一致
参考答案：C D
本题解析：加速度表示速度变化的快慢，在数值上等于单位时间内速度的变化量，只要加速度方向与速度方向相同，速度就会增大，匀速直线运动中加速度等于零，但速度不为零，AB错；
本题难度：简单