时间:2017-09-23 22:26:38
1、简答题 如图中的MN为水平放置的带电平行板,间距为d,电势差为U,两板间有磁感强度为B,方向垂直纸面向里的匀强磁场,某时刻,一个质量为m,带电量为q的负电荷,从N板的P点由静止开始进入正交电磁场中,当它经过轨迹的最高点位置K时,正好与原来静止在K点的,质量为m中性油滴相结合,随之从K点开始作匀速直线运动,(重力不计)求
(1)电荷与油滴结合后速度多大?
(2)电荷到达K点与油滴作用前的速度多大?
(3)电荷与油滴作用过程中损耗的机械能为多少?
(4)K点到N板距离多少
参考答案:(1)? ?(2)
?(2) ? (3)
? (3) ?(4)
?(4)
本题解析:
本题难度:一般
2、选择题 如图所示,竖直放置的平行板电容器,A板接电源正极,B板接电源负极,在电容器中加一与电场方向垂直的、水平向里的匀强磁场。一批带正电的微粒从A板中点小孔C射入,射入的速度大小方向各不相同,考虑微粒所受重力,微粒在平行板A、B间运动过程中(? )
A.所有微粒的动能都将增加
B.所有微粒的机械能都将不变
C.有的微粒可以做匀速圆周运动
D.有的微粒可能做匀速直线运动
参考答案:D
本题解析:带电微粒受到重力、洛伦兹力和电场力。若速度较大,则洛伦兹力向上且可能大于重力,此时将向上偏,洛伦兹力不做功,重力做负功,电场力做正功,则动能可能不变,可能减小,也可能增大,若速度较小,则洛伦兹力可能小于重力,微粒将向下偏,重力做正功,电场力做正功,动能一定增大,选项A错误.由于除重力以外的电场力对微粒做了功,机械能不守恒,故选项B错误。因液滴重力与电场力不可能平衡,所以粒子不可能做匀速圆周运动,选项C错误。若洛伦兹力与重力、电场力三力平衡,粒子可能做匀速直线运动,选项D正确.故选D.
本题难度:一般
3、填空题 1932年,著名的英国物理学家狄拉克,从理论上预言磁单极子是可以独立存在的。他认为:“既然电有基本电荷——电子存在,磁也应该有基本磁荷——磁单极子存在。”假设在真空玻璃盒内有一固定于地面上空附近的S极磁单极子,其磁场分布与负电荷电场分布相似,周围磁感线呈均匀辐射式分布,如图所示。一质量为m,电荷量为q的点电荷P在磁单极子的正上方h高处的水平面内做半径为r的匀速圆周运动。对该电荷的分析正确的是(已知地球表面的重力加速度g)
A.该电荷一定带负电荷
B.该电荷一定带正电荷
C.可确定电荷运动的速率v
D.可确定电荷运动的圆周上各处的磁感应强度B
参考答案:CD
本题解析:如图,电荷做匀速圆周运动,受到重力和洛伦兹力的合力始终指向圆心,若电荷带正电,根据左手定则可知电荷在P处的速度方向垂直纸面向里,同理若电荷带负电,电荷在P处的速度方向垂直纸面向外,故A、B均错;由于圆半径r及圆心到磁单极子的高度h已知,故θ可确定,由水平方向的牛顿第二定律、向心力公式可确定粒子的向心加速度a=gtanθ=m,因此可确定电荷运动的速率,C对;由竖直方向的平衡条件Bqvsinθ=mg,因此可确定电荷运动的圆周上各处的磁感应强度B,D对。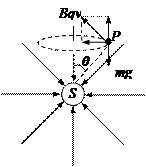
【评析】1、知识点考查:(1)匀速圆周运动,向心力,向心力公式,共点力的平衡,牛顿第二定律;(2)洛伦兹力,左手定则。
2、能力考查:(1)理解能力;(2)推理能力;(3)分析综合能力、空间想象能力
3、命题立意
(1)本题命题的起源来教材中的阅读材料——寻找磁单极子。
(2)近三年高考中对带电粒子在磁场中的偏转的考查主要设置在计算题中,且对磁偏转的考查比较单一。(3)本题对受力要求较高,特别是应用左手定则判断正、负电荷受到洛伦兹力的方向,虽然基础,但空间想象能力要求较高。
本题难度:一般
4、计算题 在竖直平面内建立一平面直角坐标系xoy,x轴沿水平方向,如图甲所示.第二象限内有一水平向右的匀强电场,第一象限内有竖直向上的匀强电场,场强 ,该区域同时存在按如图乙所示规律变化的磁场,磁场方向垂直纸面(以垂直纸面向外的磁场方向为正方向).某种发射装置(图中没有画出)竖直向上发射出一个质量为m、电荷量为q的带正电粒子(可视为质点),该粒子以v0的速度从-x上的A点进入第二象限,并从+y上的C点沿水平方向进入第一象限.已知OA=OC=L, CD=
,该区域同时存在按如图乙所示规律变化的磁场,磁场方向垂直纸面(以垂直纸面向外的磁场方向为正方向).某种发射装置(图中没有画出)竖直向上发射出一个质量为m、电荷量为q的带正电粒子(可视为质点),该粒子以v0的速度从-x上的A点进入第二象限,并从+y上的C点沿水平方向进入第一象限.已知OA=OC=L, CD= L.
L.

(1)试证明粒子在C点的速度大小也为v0;
(2)若在 时刻粒子由C点进入第一象限,且恰能通过同一水平线上的D点,速度方向仍然水平,求由C到达D的时间(时间用
时刻粒子由C点进入第一象限,且恰能通过同一水平线上的D点,速度方向仍然水平,求由C到达D的时间(时间用 ?表示);
?表示);
(3)若调整磁场变化周期,让粒子在 时刻由C点进入第一象限,且恰能通过E点,求交变磁场磁感应强度B0应满足的条件.
时刻由C点进入第一象限,且恰能通过E点,求交变磁场磁感应强度B0应满足的条件.
参考答案:(1)见解析(2)  或
或 ?(3)
?(3) 
本题解析:(1)竖直方向 ,?(2分)
,?(2分)
水平方向 ?(2分)
?(2分)
电场强度 ?(1分)
?(1分)
(2)因为 ,所以带电的粒子在第一象限将做速度也为
,所以带电的粒子在第一象限将做速度也为 匀速圆周运动, 使粒子从C点运动到同一水平线D点,如图所示,则有:
匀速圆周运动, 使粒子从C点运动到同一水平线D点,如图所示,则有: ?(2分)
?(2分) ?
?
由于CD= L,OC="L," 即
L,OC="L," 即 ,?(2分)
,?(2分)
因此,由C到达D的时间 或
或 ?(2分)
?(2分)
(3)设粒子运动圆轨道半径为R,则 ?(2分)
?(2分)
使粒子从C点运动到E点,如图所示,
 ,
, ?(3分)
?(3分)
交变磁场磁感应强度B0应满足的关系 ,
, ?(2分)
?(2分)
点评:此题的综合性较强,难度较大,需要对粒子在各个过程中受力清楚,结合相应的规律分析解题
本题难度:一般
5、选择题 如图,为磁流体发电机的示意图.金属板M、N之间的间距为d,板间有垂直纸面向里、磁感应强度大小为B的匀强磁场,将一束等离子体(即高温下电离的气体,含有大量带正电和带负电的微粒,而从整体来说呈中性)以速度v从左侧喷射入磁场,这时金属板上就会聚集电荷,产生电压.则下列说法中正确的是( )
A.金属板M上聚集负电荷,金属板N上聚集正电荷
B.通过电阻R的电流方向由a到b
C.通过电阻R的电流方向由b到a
D.该发电机的电动势E=Bdv
参考答案:A、由左手定则知正离子向上偏转,所以M带正电,A错误;
B、M板相当于电源的正极,开关闭合时,流过R的电流方向是从a至b,故B正确,C错误;
D、两板间电压稳定时满足:qvB=qE=qEd,所以E=Bdv,即发电机的电动势E=Bdv,故D正确;
故选:BD.
本题解析:
本题难度:简单