时间:2017-08-25 12:50:19
1、选择题 如图所示，一电子沿Ox轴射入电场，在电场中的运动轨迹为OCD，已知
，电子过C、D两点时竖直方向的分速度为vCy和vDy；电子在OC段和OD动能变化量分别为△Ek1和△Ek2，则
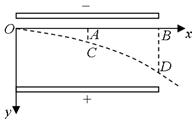
A．
B．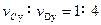
C．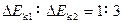
D．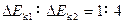
2、选择题 如图所示，一平行板电容器中存在匀强电场，电场沿竖直方向。两个比荷（即粒子的电荷量与质量之比）不同的带正电的粒子a和b，从电容器边缘的P点以相同的水平速度射入两平行板之间。测得a和b与电容器的撞击点到入射点之间的水平距离之比为1∶2。若不计重力，则a和b的比荷之比是 
[? ]
A．1∶2
B．1∶1
C．2∶1
D．4∶1
3、计算题 如图所示，有一放射源可以沿轴线ABO方向发射速度大小不同的粒子，粒子质量均为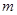
，带正电荷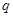
。A、B是不加电压且处于关闭状态的两个阀门，阀门后是一对平行极板，两极板间距为
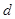，上极板接地，下极板的电势随时间变化关系如图（b）所示。O处是一与轴线垂直的接收屏，以O为原点，垂直于轴线ABO向上为
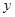轴正方向，不同速度的粒子打在接收屏上对应不同的坐标，其余尺寸见图（a），其中
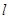和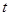
均为已知。已知
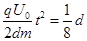，不计粒子重力。
（1）某时刻A、B同时开启且不再关闭，有一个速度为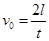
的粒子恰在此时通过A阀门，以阀门开启时刻作为图（b）中的计时零点，试求此粒子打在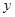轴上的坐标位置（用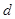表示）。
（2）某时刻A开启，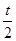
后A关闭，又过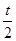后B开启，再过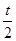后B也关闭。求能穿过阀门B的粒子的最大速度和最小速度。
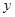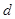（3）在第二问中，若以B开启时刻作为图（b）中的计时零点，试求解上述两类粒子打到接收屏上的坐标（用表示）。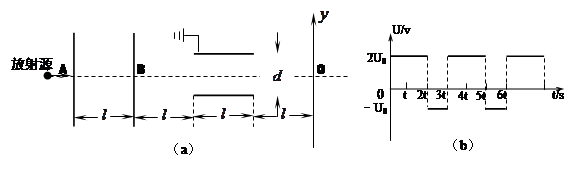
4、选择题 有三个质量相等．分别带正电、负电和不带电的小球，均从极板左侧两极板的正中央以相同的水平速度先后垂直射人匀强电场中，A、B、C三个小球的运动轨迹如图所示，小球所受重力不能忽略，则
A．小球带负电，B不带电，C带正电
B．三小球在电场中运动的时间相等
C．三小球在电场中的加速度大小关系为
D．到达正极板三小球的动能关系为
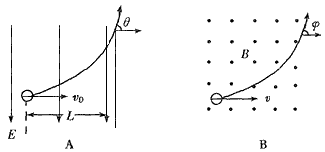
5、计算题 汤姆生在测定阴极射线荷质比时采用的方法是利用电场、磁场偏转法，即测出阴极射线在匀强电场或匀强磁场中穿过一定距离时的偏角。设匀强电场的电场强度为E，阴极射线垂直电场射入，穿过水平距离L后的运动偏角为θ（θ较小，θ≈tanθ，如图A所示）；以匀强磁场B代替电场，测出经过同样长的一段弧长L的运动偏角为φ （如图B），试以E、B、L、θ、φ表示组成阴极射线粒子比荷q／m的关系式。 