时间:2017-08-25 12:21:13
1、计算题 如图所示,在光滑水平桌面上放有长木板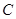 ,
,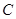 的右端有固定挡板
的右端有固定挡板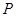 ,木板
,木板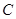 的长度为
的长度为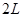 。另有小物块
。另有小物块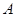 和
和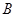 可以在长木板上滑动,
可以在长木板上滑动,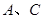 之间和
之间和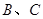 之间的动摩擦因数相同,
之间的动摩擦因数相同,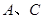 之间和
之间和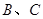 之间的最大静摩擦力等于滑动摩擦力。
之间的最大静摩擦力等于滑动摩擦力。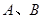 的尺寸以及
的尺寸以及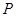 的厚度皆可忽略不计,
的厚度皆可忽略不计,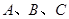 (连同挡板
(连同挡板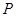 )的质量皆为
)的质量皆为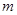 。(1)若
。(1)若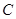 被固定在桌面上,
被固定在桌面上,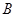 静止放在木板
静止放在木板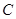 的中央,
的中央,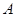 以初速度
以初速度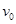 从左端冲上木板
从左端冲上木板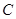 ,物块
,物块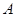 刚好能碰到
刚好能碰到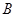 ,求
,求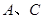 之间的动摩擦因数;(2)若
之间的动摩擦因数;(2)若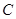 未被固定在桌面上,开始时
未被固定在桌面上,开始时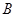 静止放在木板
静止放在木板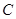 的中央,
的中央,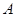 以初速度
以初速度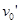 从左端冲上木板
从左端冲上木板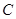 。a.要使物块
。a.要使物块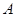 与
与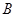 能相碰,初速度
能相碰,初速度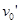 应满足的条件是什么?b.若物块
应满足的条件是什么?b.若物块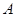 与
与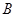 发生碰撞过程的时间极短,且碰撞过程中没有机械能损失,要使物块
发生碰撞过程的时间极短,且碰撞过程中没有机械能损失,要使物块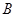 能够与挡板
能够与挡板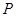 发生碰撞,初速度
发生碰撞,初速度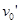 应满足的条件是什么?
应满足的条件是什么?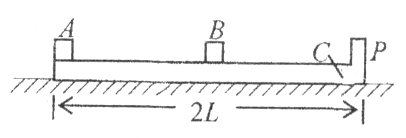
参考答案:(1)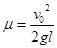 ,(2)
,(2)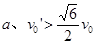 ,
,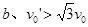
本题解析:(1)C被固定住,则A在摩擦力的作用下减速运动到B点,刚好碰到B的条件是达到B点A速度为零,即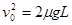 ,得
,得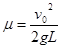
(2)a、要使物块A刚好与物块B发生碰撞,物块A运动到物块B处时,A、B的速度相等,
即v1=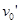 -μgt=
-μgt=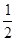 μgt?,得v1=
μgt?,得v1=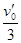 ?
?
设木板C在此过程中的位移为x1,则物块A的位移为x1+L,由动能定理?
-μmg(x1+L)=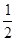 mv12-
mv12-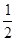 m
m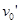 2
2
μmgx1=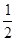 (2m)v12?
(2m)v12?
联立上述各式解得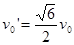 ,要使物块A、B发生相碰的条件是
,要使物块A、B发生相碰的条件是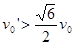
b、因为AB碰撞过程中没有机械能的损失,且两物块完全相同,所以碰撞时交换速度,就好像是A一直减速运动到挡板P一样,且刚好发生碰撞时,BC速度相等
即v2=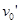 -μgt=
-μgt=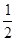 μgt?,得v2=
μgt?,得v2=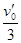
设木板C在此过程中的位移为x2,则物块AB的位移之和为x2+2L,由动能定理?
-μmg(x2+2L)=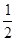 mv22-
mv22-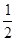 m
m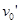 2
2
μmgx2=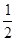 (2m)v22?
(2m)v22?
联立上述各式解得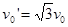 ,要使物块B与挡板发生相碰的条件是
,要使物块B与挡板发生相碰的条件是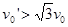
故答案为:(1)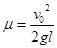 ,(2)
,(2)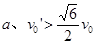 ,
,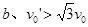
本题难度:简单
2、计算题 如图所示,在光滑的水平面上有两个并排放置木块A和B已知ma=500g、mb=300g,有一质量为80g的小铜块C以25m/s的速度开始在A表面滑动,由于C和A、B间有摩擦,C最后停在B上,和B一起以2.5m/s的速度共同向前运动,求:木块A最后的速度。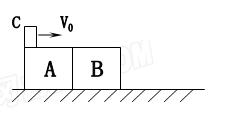
参考答案:mcv0=mAvA’+(mc+mB)v共
vA’=2.1m/s
本题解析:略
本题难度:一般
3、选择题 如图所示,一小车静止在光滑水平面上,甲、乙两人分别站在左右两侧,整个系统原来静止。则当两人同时相向走动时(? )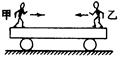
A.要使小车向左运动,甲、乙速率一定大小相等
B.要使小车静止不动,甲、乙动量大小一定大小相等
C.要使小车向左运动,甲的动量大小一定比乙的大
D.要使小车向左运动,乙的动量大小一定比甲的大
参考答案:BC
本题解析:略
本题难度:简单
4、选择题 光滑水平面上有两个质量分别是m、M的物块A、B(m<M)。第一次A以速率v0向静止的B运动,发生正碰后粘在一起共同运动;第二次B以速率v0向静止的A运动,发生正碰后粘在一起共同运动。下列判断正确的是 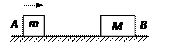
A.第一次系统末动能较小
B.第二次系统末动能较小
C.第一次系统动能损失较小
D.第二次系统动量损失较小
参考答案:A
本题解析:第一次系统初动量较小,共速时的末速度也较小,因此末动能较小。两次碰撞过程
系统的动能损失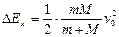 一定相同,系统动量守恒,没有动量损失。
一定相同,系统动量守恒,没有动量损失。
本题难度:一般
5、选择题 一个静止的质量为M的原子核,放射出一个质量为m的粒子,粒子速度为v,则核剩余部分的速度为( )
A.
| mv (M-m) |
| mv M |
| mv (M-m) |
| mv (M+m) |
参考答案:根据动量守恒定律研究整个原子核:
0=mv+(M-m)v′
v′=-mv(M-m)
故选C
本题解析:
本题难度:简单