时间:2017-08-25 11:45:19
1、填空题 有一条捕鱼小船停靠在湖边码头,小船又窄又长(估计重一吨左右).一位同学想用一个卷尺粗略测定它的质量,他进行了如下操作:他将船平行码头自由停泊,在岸上记下船尾的位置,然后轻轻从船尾上船.走到船头后下船,用卷尺测出几个距离,他自身的质量为m。请你回答下列问题:
参考答案:
本题解析:
本题难度:一般
2、选择题 (2011·福建理综·T29(2))在光滑水平面上,一质量为m,速度大小为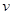 的A球与质量为2m静止的B球碰撞后,A球的速度方向与碰撞前相反。则碰撞后B球的速度大小可能是__________。(填选项前的字母)
的A球与质量为2m静止的B球碰撞后,A球的速度方向与碰撞前相反。则碰撞后B球的速度大小可能是__________。(填选项前的字母)
A.0.6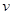
B.0.4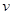
C.0.3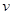
D.0.2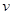
参考答案:选A.
本题解析:由动量守恒定律得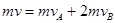 ,规定A球原方向为正方向,由题意可知vA为负值,则
,规定A球原方向为正方向,由题意可知vA为负值,则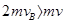 ,因此B球的速度可能为0.6v,故选A.
,因此B球的速度可能为0.6v,故选A.
本题难度:简单
3、计算题 (10分)光滑水平面上静置两个小木块1和2,其质量分别为m1=1.0kg、m2=4.0kg,它们中间用一根轻质弹簧相连。一颗水平飞行的子弹质量为m=50.0g,以v0=500m/s的速度在极短时间内射穿两木块,已知射穿木块1后子弹的速度变为原来的3/5,且子弹损失的动能为射穿木块2损失动能的2倍。求系统运动过程中弹簧的最大弹性势能。
参考答案:22.5J
本题解析:子弹与木块1系统,动量守恒mv0=m·3v0/5+m1v1?2分
同理,m·3v0/5=m·v0/5+m2v2?2分
当两小木块速度相等时(设为v),弹簧的弹性势能(E弹)最大?
m1v1+m2v2=(m1+m2)v? 2分
E弹=m1v12/2+m2v22/2-(m1+m2)v2/2? 2分
解得E弹=22.5J? 2分
本题考查动量守恒定律,当子弹打入第一个木块时,弹簧来不及被压缩,所以木块2不参与碰撞,子弹和木块1动量守恒,找到初末状态列式求解,子弹打出后打进第二个木块,子弹和木块2的动量守恒,同理列式求解,在两次碰撞前后求出子弹损失的动能,根据2倍关系列式求解
本题难度:简单
4、选择题 如图所示,在光滑水平面上有一质量为M的木块,木块与轻弹簧水平相连,弹簧的另一端连在竖直墙上,木块处于静止状态,一质量为m的子弹以水平速度v0击中木块,并嵌在其中,木块压缩弹簧后在水平面做往复运动。木块自被子弹击中前到第一次回到原来位置的过程中,木块受到的合外力的冲量大小为
A B.2Mv0 C.
B.2Mv0 C. D.2mv0
D.2mv0
参考答案:A
本题解析:从子弹击中木块到嵌入木块中,这一过程的时间极短,所以这个过程中子弹与木块组成的系统动量守恒,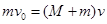 即
即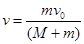 ,然后一起在水平面上做往复运动。子弹嵌入木块以后,和弹簧组成的系统机械能守恒,即动能和势能在相互转化,木块第一次回到原来位置时的速度即为子弹击中木块并和木块一起运动的速度,所以木块受到的合外力的冲量大小为
,然后一起在水平面上做往复运动。子弹嵌入木块以后,和弹簧组成的系统机械能守恒,即动能和势能在相互转化,木块第一次回到原来位置时的速度即为子弹击中木块并和木块一起运动的速度,所以木块受到的合外力的冲量大小为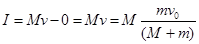 ,故A正确。
,故A正确。
考点:本题主要考查了机械能守恒定律、动量守恒定律及动能定理的应用,
点评:子弹和物块一起压缩弹簧的过程中系统机械能守恒,求出刚射入时的共同速度,子弹射入物块时间极短,瞬间子弹、物块组成的系统动量守恒,根据动量守恒即可求解
本题难度:一般
5、简答题 某同学设计了一个用打点计时器研究“动量守恒定律”的实验:在小车A的前端粘有橡皮泥,推动小车A使之做匀速运动,然后与原来静止在前方的小车B相碰并粘合成一体,继续做匀速运动,他设计的具体装置如图(a)所示,在小车A后连着纸带.
①长木板右端下面垫放一小木片的原因是______;
②若已测得打点纸带如图(b)所示,A为运动的起点,各计数点间距分别记为AB、BC、CD和DE,用天平测得A、B两车的质量分别为mA、mB.,则需验证的表达式为:______.
参考答案:(1)长木板右端下面垫放一小木片是为了平衡摩擦力,让重力沿斜面的分量平衡滑块与木板间的摩擦力;
(2)由于碰撞之后共同匀速运动的速度小于碰撞之前A独自运动的速度,故AC应在碰撞之前,DE应在碰撞之后.
推动小车由静止开始运动,故小车有个加速过程,在碰撞前做匀速直线运动,即在相同的时间内通过的位移相同,故BC段为匀速运动的阶段,故选BC计算碰前的速度;
碰撞过程是一个变速运动的过程,而A和B碰后的共同运动时做匀速直线运动,故在相同的时间内通过相同的位移,故应选DE段来计算碰后共同的速度.
碰前系统的动量即A的动量,则P1=mAvA=mABC3T
碰后的总动量P2=(mA+mB)v共=(mA+mB)DE3T
所以则需验证的表达式为:mABC3T=(mA+mB)DE3T
即mA?BC=(mA+mB)?DE
故答案为(1)平衡摩擦力;(2)mA?BC=(mA+mB)?DE
本题解析:
本题难度:一般