时间:2017-08-25 11:29:57
1、计算题 质量为m的带电液滴,在电场强度为E,方向竖直向上的匀强电场中处于静止状态,试求:(1)该液滴的带电性质和所带的电荷量;
(2)当场强方向保持不变,而大小突然减为原来的一半时,求液滴的加速度。
参考答案:(1)带正电,且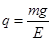 ;(2)
;(2)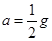
本题解析: (1)液滴处于静止状态,所受电场力竖直向上,电场也竖直向上,所以应带正电荷,由平衡条件得: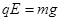 ,得
,得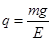 .
.
(2)场强减半后,液滴竖直向下做加速直线运动,由牛顿第二定律,有: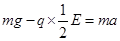 ,得
,得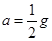 ,方向竖直向下。
,方向竖直向下。
本题难度:一般
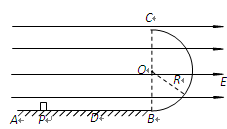
2、计算题 如图所示,水平绝缘粗糙的轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接,半圆形轨道的半径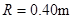 .在轨道所在空间存在水平向右的匀强电场,电场线与轨道所在的平面平行,电场强度
.在轨道所在空间存在水平向右的匀强电场,电场线与轨道所在的平面平行,电场强度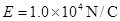 .现有一电荷量
.现有一电荷量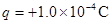 ,质量
,质量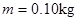 的带电体(可视为质点),在水平轨道上的P点由静止释放,带电体恰好能通过半圆形轨道的最高点C,然后落至水平轨道上的D点.取
的带电体(可视为质点),在水平轨道上的P点由静止释放,带电体恰好能通过半圆形轨道的最高点C,然后落至水平轨道上的D点.取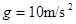 .
.
试求:
(1)带电体在圆形轨道C点的速度大小.
(2)D点到B点的距离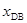 .
.
(3)带电体运动到圆形轨道B点时对圆形轨道的压力大小.
(4)带电体在从P开始运动到落至D点的过程中的最大动能。
参考答案:(1) 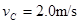 ?(2)
?(2) 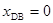 ?(3)
?(3) 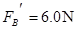 ?(4)
?(4) 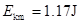
本题解析:(1)设带电体通过C点时的速度为vC,依据牛顿第二定律: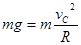 ---------------------------------1分
---------------------------------1分
解得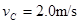 ------------------------------1分
------------------------------1分
(2)设带电体从最高点C落至水平轨道上的D点经历的时间为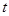 ,根据运动的分解有:
,根据运动的分解有: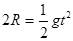 ------------------------------------1分
------------------------------------1分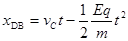 -----------------------------2分
-----------------------------2分
联立解得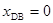 -------------------------------1分
-------------------------------1分
(3)设带电体通过B点时的速度为vB,设轨道对带电体的支持力大小为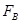 ,带电体在B点时,根据牛顿第二定律有
,带电体在B点时,根据牛顿第二定律有 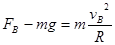 --------1分
--------1分
带电体从B运动到C的过程中,依据动能定理: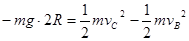 ---------------------------2分
---------------------------2分
联立解得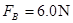 -------------------------------------1分
-------------------------------------1分
根据牛顿第三定律,带电体对轨道的压力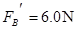 --------------1分
--------------1分
(4)由P到B带电体作加速运动,故最大速度一定出现在从B经C到D的过程中.在此过程中只有重力和电场力做功,这两个力大小相等,其合力与重力方向成45?夹角斜向右下方,故最大速度必出现在B点右侧对应圆心角为45 ?处.
设小球的最大动能为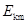 ,根据动能定理有:
,根据动能定理有: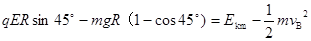 -----------2分
-----------2分
解得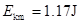 (或
(或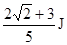 )--------------------1分
)--------------------1分
点评:做此类型的题目,需要根据圆周运动知识分析最高点或者最低点的速度,然后根据能量守恒定律分析解题
本题难度:一般
3、选择题 如图所示,水平放置的两块相同的金属板带等量异种电荷,两板间有垂直纸面向里的水平方向的匀强磁场,一带电的粒子(不计重力)在P点由静止释放,运动到A点时速度方向水平,则( )
A.从P到A,粒子的速度不变
B.从P到A,粒子竖直方向的分速度一直增大
C.从A点粒子受到的磁场力一定大于电场力
D.从A点开始粒子可能做匀速直线运动
参考答案:
对粒子进行受力分析,受电场力和洛伦兹力作用,由于粒子从静止开始运动,因此电场力方向向下,洛伦兹力的方向只能向上,由左手定则可判断出粒子带正电.
A、从P到A,受到电场力与洛伦兹力,虽然洛伦兹力不做功,但由于电场力做正功,导致粒子的速度增加,故选项A错误,
B、从P到A,粒子由于电场力做正功,则竖直方向的分速度增大,故选项B正确.
C、从A点粒子受到的磁场力可能等于电场力,因此粒子处于平衡状态,做匀速直线运动,故C错误,D正确;
故选BD
本题解析:
本题难度:一般
4、计算题 如图所示,在足够大的空间范围内,同时存在着竖直向上的匀强电场和垂直纸面向里的水平匀强磁场,磁感应强度B=1.57T。小球1带正电,其电量与质量之比q1/m1=4C/kg,所受重力与电场力的大小相等;小球2不带电,静止放置于固定和水平悬空支架上。小球1向右以v0=23.59m/s的水平速度与小球2正碰,碰后经0.75s再次相碰。设碰撞前后两小球带电情况不发生改变,且始终保持在同一竖直平面内。(g=9.8m/s2)问:
(1)电场强度E的大小是多少?
(2)两小球的质量之比是多少? 
参考答案:解:(1)小球1所受的重力与电场力始终平衡m1g=q1E① ,E=2.45N/C ②
(2)相碰后小球1做匀速圆周运动,由牛顿第二定律得: ③
③
半径为 ④ ,
④ ,
周期为 ⑤
⑤
∵两球运动时间t=0.75s= T
T
∴小球1只能逆时针经 周期时与小球2再次相碰
周期时与小球2再次相碰
第一次相碰后小球2作平抛运动h=R1= ⑥,
⑥,
L=R1=v2t?⑦
两小球第一次碰撞前后动量守恒,以水平向右为正方向m1v0=m1v1+m2v2?⑧
由⑥、⑦式得v2=3.75m/s
由④式得 v1=17.66m/s
∴两小球质量之比: =11⑨
=11⑨
本题解析:
本题难度:一般
5、计算题 (12分)如图甲所示,相隔一定距离的竖直边界两侧为相同的匀强磁场区,磁场方向垂直纸面向里,在边界上固定两长为L的平行金属极板MN和PQ,两极板中心各有一小孔S1、S2,两极板间电压的变化规律如图乙所示,电压的大小为U0,周期为T0。在t=0时刻将一个质量为m、电荷量为-q(q>0)的粒子由S1静止释放,粒子在电场力的作用下向右运动,在t=时刻通过S2垂直于边界进入右侧磁场区。(不计粒子重力,不考虑极板外的电场)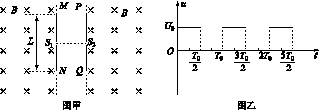
(1)求粒子到达S2时的速度大小v
(2)为使粒子不与极板相撞,求磁感应强度的大小应满足的条件;
(3)若已保证了粒子未与极板相撞,为使粒子在t=T0时刻再次到达S1,而再次进入电场被加速,求该过程中粒子在磁场内运动的时间和磁感应强度的大小。
参考答案:(1)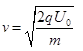 (2)B<
(2)B<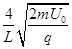 (3)
(3)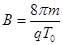
本题解析:(1)粒子由S1至S2的过程中,根据动能定理得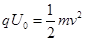 ?2分
?2分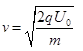 ?1分
?1分
(2)设磁感应强度大小为B,粒子在磁场中做匀速圆周运动的半径为R,由牛顿第二定律得 ?1分
?1分
要使粒子在磁场中运动时不与极板相撞,须满足2R> ?1分
?1分
得B<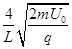 ?1分
?1分
(3)设极板间距d、粒子在两边界之间无场区向左匀速运动的过程用时为t1,有d=vt1?1分
粒子由S1至S2的过程中,粒子做匀加速直线运动有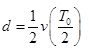 ?1分
?1分 ?1分
?1分
粒子在磁场中运动的时间为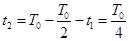 ?1分
?1分
设粒子在匀强磁场中做匀速圆周运动的周期为T,由 结合运动学公式
结合运动学公式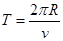 得
得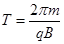 ?1分
?1分
由题意得T=t2
得 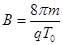 ?1分
?1分
本题难度:一般