时间:2017-08-22 02:59:07
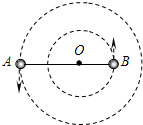
1、填空题 银河系恒星中大约有四分之一是双星．某双星系统由星球A和B组成，两星球在相互之间的万有引力作用下绕两者连线上某一定点P做匀速圆周运动．已知A和B的质量之比为mA：mB=1：2，两星球的线速度之比为vA：vB=______；若由天文观察测得A星球的周期为T，AB间距离为r，已知万有引力常量为G，则A星球的质量为mA=______．
参考答案：1、双星靠相互间的万有引力提供向心力，周期相等、加速度相等．根据GmAmB?r2=mA(2πT)2rA=mB(2πT)2rB，
则半径rA：rB=mB：mA=2：1
所以两星球的半径之比为2：1，
根据v=rω得，
vA：vB=rA：rB=mB：mA=2：1
2、因为=rA：rB=mB：mA=2：1
又rA+rB=r，
所以rA=23r，rB=13r，
A、B的周期都为T，根据双星之间的万有引力提供向心力GmAmB?r2=mB(2πT)2rB，
所以GmAr2=(2πT)2?13r
解得：mA=4π2r33GT2．
故答案为：2：1，4π2r33GT2．
本题解析：
本题难度：一般
2、简答题 游乐场的过山车可以底朝上在圆轨道上运行，游客却不会掉下来，如图甲所示．我们把这种情况抽象为如图乙所示的模型：半径为R的圆弧轨道竖直放置，下端与弧形轨道相接，使质量为m的小球从弧形轨道上端无初速度滚下，小球进入圆轨道下端后沿圆轨道运动．实验表明，只要h大于一定值，小球就可以顺利通过圆轨道的最高点．（不考虑空气及摩擦阻力）
（1）若小球恰能通过最高点，则小球在最高点的速度为多大？此时对应的h多高？
（2）若h′=4R，则小球在通过圆轨道的最高点时对轨道的压力是多少？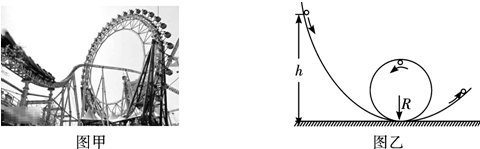
参考答案：（1）小球恰能通过最高点，即小球通过最高点时恰好不受轨道的压力，重力提供向心力．由牛顿运动定律有：
mg=mv2R
小球在最高点处的速度至少为：v=
本题解析：
本题难度：一般
3、计算题 如图所示，一根长0.1m的细线，一端系着一个质量为0.18kg的小球，拉住线的另一端，使球在光滑的水平桌面上作匀速圆周运动，使小球的转速很缓慢地增加，当小球的转速增加到开始时转速的3倍时，细线断开，线断开前的瞬间线的拉力比开始时大40N，求：
（1）线断开前的瞬间，线的拉力大小。
（2）线断开的瞬间，小球运动的线速度。
（3）如果小球离开桌面时，速度方向与桌边的夹角为60°，桌面高出地面0.8m，求小球飞出后的落地点距桌边的水平距离。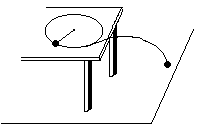 
参考答案：解：（1）线的拉力等于向心力，设开始时角速度为ω0，向心力是F0，线断开的瞬间，角速度为ω，线的拉力是F
，
则
又因为F＝F0＋40N
得F＝45N
（2）设线断开时速度为V
由F＝mV2/R，得V＝
（3）设桌面高度为h，落地点与飞出桌面点的水平距离为s
，
则抛出点到桌边的水平距离为
本题解析：
本题难度：困难
4、简答题 如图所示，在一根长1.5L的不能伸长的轻绳上，穿一个质量为m的光滑小圆环C，然后把绳的两端固定在竖直轴上，绳的A、B端在竖直轴上的距离为L/2，转动竖直轴带动C环在水平面内做匀速圆周运动，当绳的B端正好在C环的轨道平面上时，求：
（1）小圆环转动的角速度；
（2）绳的拉力．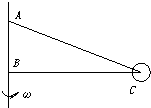
参考答案：
（1）环C在水平面内做匀速圆周运动，由于环光滑，所以环两端绳的拉 力大小相等．BC段绳水平时，环C做圆周运动的半径r=.BC，
则有：r2+(L2)2=(1.5L-r)2
解得：r=2L3
环的受力如图所示，则：
Fsinα=mg
Fcosα+F=mω2r
又sinα=35、sinα=35
解得：ω=3
本题解析：
本题难度：一般
5、简答题 神奇的黑洞是近代引力理论所预言的一种特殊天体，探寻黑洞的方案之一是观测双星系统的运动规律．天文学家观测河外星系麦哲伦云时，发现了LMCX-3双星系统，它由可见星A和不可见的暗星B构成，两星视为质点，不考虑其它天体的影响，A、B围绕两者的连线上的O点做匀速圆周运动，它们之间的距离保持不变，如图所示，引力常量为G，由观测能够得到可见星A的速率v和运行周期T．
（1）可见星A所受暗星B的引力FA可等效为位于O点处质量为m"的星体（视为质点）对它的引力，设A和B的质量分别为m1、m2．试求m′（用m1、m2表示）
（2）求暗星B的质量m2与可见星A的速率v、运行周期T和质量m1之间的关系式．
参考答案：（1）设A、B的圆轨道半径分别为r1、r2，由题意知，A、B做匀速圆周运动的角速度相同，其为ω．
由牛顿运动定律，
对A：FA=m1ω2r1?对B：FB=m2ω2r2?FA=FB
设A、B之间的距离为r又r=r1+r2，由上述各式得r=m1+m2m2r1①
由万有引力定律，有FA=Gm1m2r2
将①代入得FA=Gm1m32(m1+m2)2r2
令FA=Gm1m′r12
比较可得m′=m32(m1+m2)2②
（2）根据题意，可见星A所受暗星B的引力FA可等效为位于O点处质量为m"的星体对它的引力，由牛顿第二定律，有Gm1m′r12=m1v2r1③
得? m′=r1v2G④
又可见星A的线速度大小v=2πr1T⑤
由④⑤得，m′=v3T2πG
由②⑤可得m32(m1+m2)2=v3T2πG
答：（1）O点处星体质量为m′为m32(m1+m2)2．
? （2）暗星B的质量m2与可见星A的速率v、运行周期T和质量m1之间的关系式为v3T2πG
本题解析：
本题难度：一般