时间:2017-08-22 02:23:37
1、简答题 如图所示，用两根长度都为L的细绳悬挂一个小球A，绳与水平方向的夹角为a ．使球A垂直于纸面做摆角小于10°的摆动，当它经过平衡位置的瞬间，另一小球B从A球的正上方自由下落，若B球恰能击中A球，求B球下落的高度．
参考答案：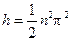
Lsina ，其中n＝1，2，3
本题解析：单摆的振动周期公式为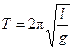
，据题意l＝Lsina （2分），
所以A球振动的周期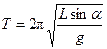
?．（2分）
设球B自由下落的时间为t，则它击中A球下落的高度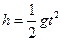
，
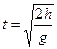（2分）
球A经过平衡位置，接着返回到平衡位置的时间为半个周期，即
B球能击中A球的时间应为A球做简谐振动的半周期的整数倍，即
故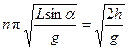
（4分，未考虑周期性给2分）
则B球下落的高度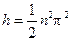Lsina ，其中n＝1，2，3…（3分，未考虑周期性给1分）
本题难度：简单
2、实验题 A、B两物体做简谐运动,在A物体振动20次的时间内,B物体振动15次,A、B两物体振动的周期之比为___________,频率之比为___________.若要求A、B都振动20次,需要的时间之比是___________.
参考答案：3∶4? 4∶3? 3∶4
本题解析：设t时间内A物体振动20次,则B物体振动15次,两周期之比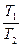
=
/
=
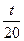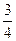,又因为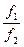
=
,所以频率之比=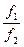
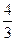.若A、B都振动20次,A所需的时间tA=20×TA,B所需要的时间tB=20×TB,所以
=
=.
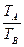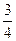本题难度：简单
3、实验题 房顶上固定着一根不可伸长的细线，下垂到三楼窗沿下，某同学应用单摆原理测量窗的上沿到房顶的高度，先将线的下端系上一个小球，发现当小球静止时，细线恰好与窗子上沿接触且保持竖直，他打开窗子，让小球在垂直于墙的竖直平面内摆动，如图所示，从小球第1次通过图中的B点开始计时，第21次通过B点用时30s；球在最低点B时，球心到窗上沿的距离为1m，当地重力加速度取g=π2（m/s2）；根据以上数据可得小球运动的周期T=_______s；房顶到窗上沿的高度h=_______m。
参考答案：3(3分)? 3(3分)
本题解析：因为是从小球第1次通过图中的B点开始计时，故第21次通过B点为10个周期，则周期为
；
根据周期公式有：
，l1=1m，代入得：l2=4m，则房顶到窗上沿的高度h=3m。
本题难度：一般
4、简答题 在同一地点有甲、乙两个单摆，当甲完成8次全振动时，乙摆在相同时间内完成6次全振动．若甲摆的摆长比乙摆的摆长短70厘米，求甲、乙两摆的摆长．
参考答案：设甲完成8次全振动所经历的时间为t，则
? T甲=t8，T乙=t6
得到T甲：T乙=3：4
又因为T甲=2π
本题解析：
本题难度：一般
5、选择题 在同一地点，两个单摆的摆长之比为1：4，则它们的频率之比为（ ）
A．1：4
B．1：2
C．4：1
D．2：1
参考答案：根据单摆的周期公式T=2π
本题解析：
本题难度：简单