时间:2017-08-22 01:45:40
1、选择题 据报道，天文学家近日发现了一颗距地球40光年的“超级地球”，名为“55
Cancri e”，该行星绕母星(中心天体)
运行的周期约为地球绕太阳运行周期的
，母星的体积约为
太阳的60倍。假设母星与太阳密度相同，“55Cancri e”与地球均做匀速圆周运动，则“55 Cancri e”与地球的
[? ]
A．轨道半径之比约为
B．轨道半径之比约为
C．向心加速度之比约为
D．向心加速度之比约为
参考答案：B
本题解析：
本题难度：一般
2、选择题 （8分）某行星的半径为R，它有一颗卫星，卫星绕它公转的轨道半径为r、公转周期为T．万有引力常量为G.求该行星的质量和密度。
参考答案：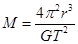
，
本题解析：（1）万有引力提供卫星做半径为r的圆周运动，则：
?
?（4分）
（2）该天体的体积为：
?（4分）
本题难度：一般
3、选择题 据新闻报道：“嫦娥二号”探月卫星于2010年10月1日18时成功发射。卫星绕月运行的圆形轨道距月球表面约为100km,用118分钟绕月球运行一周，运行速度约1.6km/s。已知万有引力常量
，由以上信息可以估算下面哪些物理量
A.月球半径?B月球的自转周期
C.“嫦娥二号”卫星的质量?D.月球表面重力加速度
参考答案：AD
本题解析：由公式
得
，再根据公式
得
，
联立可得月球半径，A正确，根据题中的信息无法求出月球的自转周期，B错误
因为计算过程中卫星的质量消去了，所以也无法求出卫星的质量，C错误，
由公式
得
，结合上述几个式子可得重力加速度，D正确
故选AD
点评：应用万有引力定律进行卫星加速度、速度、周期和中心天体质量的估算
本题难度：一般
4、选择题 有一双星各以一定的速率绕垂直于两星连线的轴转动，两星与轴的距离分别为R1和R2，转动周期为T，那么下列说法中错误的是（ ）
A．这两颗星的质量必相等
B．这两颗星的质量之和为
| 4π2(R1+R2)3 GT2 |
| m1 m2 |
| R2 R1 |
| 4π2R1(R1+R2)2 GT2 |
参考答案：
A：对m1有：Gm1m2(R1+R2)2=m1R14π2T2，解得：m2=4π2R1(R1+R2)2GT2，同理可得：m1=4π2R2(R1+R2)2GT2，故两者质量不相等，故A错误
B：由A两者质量相加得：4π2(R1+R2)3GT2，故B正确
C：由A知m1：m2=R2：R1故C正确．
D：由A知m2=4π2R1(R1+R2)2GT2，故D正确．
本题选错误的，故选：A
本题解析：
本题难度：简单
5、简答题 2007年10月24日，中国首颗探月卫星“嫦娥一号”在西昌卫星发射中心发射升空，准确进入预定轨道．随后，“嫦娥一号”经过变轨和制动成功进入环月轨道．如图所示，阴影部分表示月球，设想飞船在距月球表面高度为3R的圆形轨道Ⅰ上作匀速圆周运动，到达A点时经过暂短的点火变速，进入椭圆轨道Ⅱ，在到达轨道Ⅱ近月点B点时再次点火变速，进入近月圆形轨道Ⅲ，而后飞船在轨道Ⅲ上绕月球作匀速圆周运动．已知月球半径为R，月球表面的重力加速度为g0，引力常量为G．不考虑其它星体对飞船的影响，求：
（1）飞船在轨道Ⅰ、Ⅲ的速度之比．
（2）飞船在轨道Ⅰ上的运动周期．
（3）飞船从轨道Ⅱ上远月点A运动至近月点B所用的时间．
参考答案：（1）在轨道I有GMm(4R)2=mv214R （1）
在轨道II上有GMmR2=mv2mR（2）
（1）÷（2）得：v1vm=12
（2）设飞船在轨道I上的运动周期为T1，在轨道I有
GMm(4R)2=m4π2T214R（3）
在月球表面有 GMmR2=mg1 （4）
联立（3）（4）解得：T1=16π
本题解析：
本题难度：一般