时间:2015-06-10 22:40:09
则当![]() 时,
时,![]() ,符合题意;
,符合题意;
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 单调递减,而
单调递减,而![]() ,
,
则当![]() 时,
时,![]() ,不符合题意;
,不符合题意;
当![]() 时,设
时,设![]() ,当
,当![]() 时
时 ,
,
![]() 在
在![]() 单调递增,因此当
单调递增,因此当![]() 时
时![]() ,
,
于是![]() ,当
,当 时
时![]() ,
,
此时![]() ,不符合题意.
,不符合题意.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.
另解:(Ⅰ)![]() ,定义域为
,定义域为![]()
 ,
,
当![]() 时,
时, ,函数
,函数![]() 在
在![]() 为增函数,无极值点.
为增函数,无极值点.
设![]() ,
,
当![]() 时,根据二次函数的图像和性质可知
时,根据二次函数的图像和性质可知![]() 的根的个数就是函数
的根的个数就是函数![]() 极值点的个数.
极值点的个数.
若![]() ,即
,即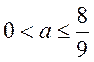 时,
时,![]() ,
,![]() 函数在
函数在![]() 为增函数,无极值点.
为增函数,无极值点.
若![]() ,即
,即 或
或![]() ,
,
而当![]() 时
时![]() 此时方程
此时方程![]() 在
在![]() 只有一个实数根,此时函数
只有一个实数根,此时函数![]() 只有一个极值点;
只有一个极值点;
当 时方程
时方程![]() 在
在![]() 都有两个不相等的实数根,此时函数
都有两个不相等的实数根,此时函数![]() 有两个极值点;
有两个极值点;
综上可知当 时
时![]() 的极值点个数为0;当
的极值点个数为0;当![]() 时
时![]() 的极值点个数为1;当
的极值点个数为1;当 时,
时,![]() 的极值点个数为2.
的极值点个数为2.
(Ⅱ)设函数![]() ,
,![]() ,都有
,都有![]() 成立.
成立.
即![]()
当![]() 时,
时,![]() 恒成立;
恒成立;
当![]() 时,
时,![]() ,
, ;
;
当![]() 时,
时,![]() ,
,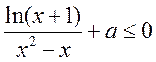 ;由
;由![]() 均有
均有![]() 成立。
成立。
故当![]() 时,,
时,,
![]() ,则只需
,则只需![]() ;
;
当![]() 时,
时, ,则需
,则需![]() ,即
,即![]() .综上可知对于
.综上可知对于![]() ,都有
,都有![]() 成立,只需
成立,只需![]() 即可,故所求
即可,故所求![]() 的取值范围是
的取值范围是![]() .
.
另解:设函数![]() ,
,![]() ,要使
,要使![]() ,都有
,都有![]() 成立,只需函数函数
成立,只需函数函数![]() 在
在![]() 上单调递增即可,
上单调递增即可,
于是只需![]() ,
,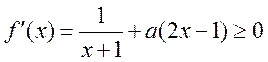 成立,
成立,
当 时
时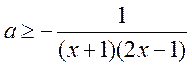 ,令
,令![]() ,
, ,
,
则![]() ;当
;当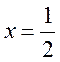 时
时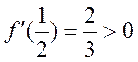 ;当
;当 ,
, ,
,
令![]() ,
,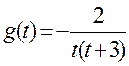 关于
关于![]() 单调递增,则
单调递增,则 ,则
,则![]() ,于是
,于是![]() .
.
又当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 单调递减,而
单调递减,而![]() ,
,
则当![]() 时,
时,![]() ,不符合题意;
,不符合题意;
当![]() 时,设
时,设![]() ,当
,当![]() 时
时 ,
,
![]() 在
在![]() 单调递增,因此当
单调递增,因此当![]() 时
时![]() ,
,
于是![]() ,当
,当 时
时![]() ,
,
此时![]() ,不符合题意.
,不符合题意.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.






