时间:2015-05-02 21:13:46
） [来源:学科网]
常用的导数运算法则：
法则1：
法则2：
法则3：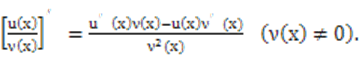
3、导数在研究函数中的应用
(1)了解函数的单调性与导数的关系；能利用导数研究函数的单调性，会求函数的单调区间(对多项式函数不超过三次)。
(2)了解函数在某点取得极值的必要条件和充分条件；会用导数求函数的极大值、极小值(对多项式函数不超过三次)；会求闭区间上函数的最大值、最小值(对多项式函数不超过三次)。
(3)会用导数解决实际问题。
(十七)统计案例
了解下列一些常见的统计方法，并能应用这些方法解决一些实际问题。
1、独立性检验
了解独立检验（只要求2*2列联表）的思想、方法及其简单应用。
2、回归分析
了解回归分析的基本思想、方法及其简单的应用。
(十八)推理与证明
1、合情推理与演绎推理
(1)了解合情推理的含义，能利用归纳和类比进行简单的推理，了解合情推理在数学发现中的作用。
(2)了解演绎推理的重要性，掌握演绎推理的基本模式，并能运用它们进行一些简单演绎推理。了解合情推理和演绎推理之间的联系和差异。
2、直接证明与间接证明
(1)了解直接证明的两种基本方法：综合法和分析法；了解综合法和分析法的思考过程和特点。
(2)了解间接证明的一种基本方法——反证法，了解反证法的思考过程和特点。
(十九)数系的扩充和复数的引入
1、复数的概念
(1)理解复数的基本概念，理解复数相等的充要条件。
(2)了解复数的代数表示法及其几何意义。
2、复数的四则运算[来源:Zxxk.Com]
能进行复数代数形式的四则运算，了解复数代数形式的加、减运算的几何意义。
(二十)框图
1、流程图
（1）了解程序框图。
(2)了解工序流程图（即统筹图）。
（3）能绘制简单实际问题的流程图，了解流程图在解决实际问题中的作用。
2、结构图
（1）了解结构图。
（2）会运用结构图梳理已学过的知识结构，整理收集到的资料信息。
III.考试形式与试卷结构
考试采用闭卷、笔试的形式。全卷满分为150分，考试时间为120分钟。全卷分为第I卷和第II卷两部分，第I卷为选择题，第II卷为非选择题，全部为必考内容。
整卷共20-22题，含选择题、填空题和解答题三种题型。选择题四选一型的单选题；填空题只要求直接填写结果，不必写出计算或推理过程；解答题包括计算题、证明题和应用题等，解答题应写出文字说明、演算步骤或推证过程。三种题型分数的百分比约为：选择题和填空题共50%左右，解答题50%左右。
试卷应有合理的知识结构（数学各部分知识在试卷中所占的比例），使得考查各部分内容基本符合普通高等学校对考生的要求，考查选修系列1的内容约占25%。
试题应用合理的能力层次结构（试卷对能力要求的层次和占分比例），使得对能力要求的层次和占分比例符合普通高等学校对考生的要求。
试题按相对难度即得分率（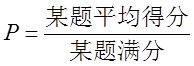
）分为容易题（P为0.7以上）、中等难度题（P为0.4 -0.7）、难题（P为0.4以下）。试卷应设计合理的难易结构（包括各题型的难度结构）。应发挥各种题型的区分选拔功能，每种题型原则上按由易到难的顺序排列，以有利于考生稳定应考情绪，正常发挥考试水平。试卷以中等难度题为主，总体难度要适当。
IV.题型示例（文科）
为了更好地理解考试内容和要求，特编制下列题型示例（题型示例由近年高考试题组成）
供参考，所列样题力求体现试题的各种题型及难度，它与考试时试题的题序安排、考查内容、难度没有对应关系。
示例 略
对例题部分例题进行了更换，引入了2014年各地高考真题。所举例题数目没变；选择题举例30道，填空题举例15道，解答题举例18道。附录改为2014年安徽数学文科典型试题分析。
考点变动情况见上文，红色部分代表相对于2014年考纲的变动情况，红字为增加部分。增加了 几何概型 考点。
安徽高考考试说明·文理科数学区别
|
理科数学 |
文科数学 |
|
（一） 知识要求 知识是指《课程标准》所规定的必修课程、选修系列2和系列4中4-4和4-5的数学概念、性质、法则、公式、公理、定理以及由其内容反映的数学思想和方法 |
（一） 知识要求 知识是指《课程标准》所规定的必修课程、选修系列1中的数学概念、性质、法则、公式、公理、定理以及由其内容反映的数学思想方法
|
|
5 （2）根据具体函数的图象，能够用二分法求相应方程的近似解。 |
无此考点 |
|
2．古典概型 (2)会计算一些随机事件所含的基本事件数及事件发生的概率。 |
2．古典概型 (2)会用列举法计算一些 |
|
(十五)圆锥曲线与方程 (2)掌握抛物线的定义、几何图形、标准方程和简单的几何性质。
|
(十五)圆锥曲线与方程 (4)了解抛物线的定义、几何图形和标准方程，知道其简单的几何性质。 |
|
2、曲线与方程 了解方程的曲线与曲线的方程的对应关系。
|
无此考点 |
|
(十六)空间向量与立体几何 1、空间向量及其运算 （1）了解空间向量的概念，了解空间向量的基本定理及其意义，掌握空间向量的正交分解及其坐标表示。 （2）掌握空间向量的线性运算及其坐标表示。 （3）掌握空间向量的数量积及其坐标表示，能用向量的数量积判断向量的共线和垂直。 2、空间向量的应用 （1）理解直线的方向向量及其平面的法向量。 （2）能用向量语言表述直线和直线、直线与平面、平面与平面的垂直、平行关系。 （3）能用向量方法证明有关直线和平面位置关系的一些定理（包括三垂线定理）。 （4）能用向量方法解决直线与直线、直线与平面、平面与平面的夹角计算问题，了解空间向量方法在研究立体几何问题中的作用。
|
无此考点 |
|
理科数学 |
文科数学 |
|
2、导数的运算 (1)能根据导数的定义求函数y=C(C为常数)，y=x, |
删去 y=x3 ， |
|
2、导数的运算 (2)能利用以下给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数，能求简单的符合函数（仅限于形如 |
删去
|
|
5、定积分与微积分基本定理 （1）了解定积分的实际背景，了解定积分的基本思想，了解定积分的概念。 （2）了解微积分基本定理的含义 |
无此考点 |
|
（3）数学归纳法 了解数学归纳法的原理，能用数学归纳法证明一些简单的数学命题。 |
无此考点 |
|
(二十)计数原理 1、分类加法计数原理、分步乘法计数原理 理解分类加法计数原理和分步乘法计数原理。会用分类加法计数原理或分步乘法计数原理分析和解决一些简单的实际问题。 2、排列与组合 理解排列、组合的概念。能利用计数原理推导排列数、组合数公式，并能利用公式解决一些简单的实际问题。 3、二项式定理 （1）能用计数原理证明二项式定理。 （2）会用二项式定理解决与二项式展开式有关的简单问题。 |
无此考点 |
|
1、概率 （1）理解取有限个值的离散型随机变量及其分布列的概念，了解分布列队于刻画随机现象的重要性。 （2）了解条件概率和两个事件相互独立的概念，理解n次独立重复试验模型及二项分布，并能解决一些简单的实际问题。 （3）理解取有限个值的离散型随机变量的均值、方差的概念，能计算简单离散型随机变量的均值、方差，并能解决一些实际问题。 （4）利用实际问题的直方图，了解方态分布曲线的特点及曲线所表示的意义。 |
无此考点 |
|
理科数学 |
文科数学 |
|
(二十二)坐标系与参数方程 1、 坐标系 （1）理解坐标系的作用。 （2）了解在平面直角坐标系伸缩变换作用下平面图形的变化情况。 （3）能在极坐标系中用极坐标表示点的位置，理解在极坐标系和平面直角坐标系中表示点的位置的区别，能进行极坐标和直角坐标的互化。 （4）能在极坐标系中给出简单图形（如过极点的直线、过极点或圆心在极点的圆）的方程。通过比较这些图形在极坐标系和平面直角坐标系中的方程，理解用方程表示平面图形时选择适当坐标系的意义。 2、参数方程 （1）了解参数方程，了解参数的意义。 （2）能选择适当的参数写出直线、圆和椭圆曲线的参数方程。 |
无此考点 |
|
(二十三)不等式选讲 1.理解绝对值的几何意义，并能利用含绝对值不等式的几何意义证明以下不等式： （1） （2） 2.会利用绝对值的几何意义求解以下类型的不等式： 了解证明不等式的基本方法：比较法、综合法、分析法、反证法、放缩法。 |
无此考点 |
|
没单独表述此考点 |
(二十)框图 1、流程图 （1）了解程序框图。 (2)了解工序流程图（即统筹图）。 （3）能绘制简单实际问题的流程图，了解流程图在解决实际问题中的作用。 2、结构图 （1）了解结构图。 （2）会运用结构图梳理已学过的知识结构，会整理收集到的资料信息。 |
|
考查选修系列2和选修系列4的内容约占35% |
考查选修系列1的内容约占25% |
的导数。
的复合函数）的导数。
