时间:2015-05-02 20:28:28
事件的独立性
√
n次独立重复试验与二项分布
√
取有限值的离散型随机变量的均值
√
考试采用闭卷、笔试形式.考试时不允许使用计算器.
考试时间为120分钟,试卷满分为150分.
全卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
试卷结构如下:
|
卷别 |
题型 |
题数 |
分值 |
说明 |
|
第Ⅰ卷 |
选择题 |
10 |
50 |
四选一型的单项选择 |
|
第Ⅱ卷 |
填空题 |
5 |
25 |
只需直接填写结果,不必写出具体解答过程 |
|
解答题 |
6 |
75 |
要求写出必要的文字说明、演算步骤或证明过程 |
试题按其难度分为容易题、中等难度题和难题.难度系数在0.7以上的试题为容易题,难度系数为0.4~0.7的试题是中等难度题,难度系数在0.4以下的试题为难题.试卷由三种难度的试题组成,并以中等难度题为主.命题时根据有关要求和教学实际合理控制容易题、中等难度题和难题三种试题的分值比例及全卷总体难度.![]()
一、选择题
1.设集合![]() ,
,![]() ,则集合
,则集合![]() 等于
等于
(A){-2} (B){2}
(C){-2,2} (D)![]()
2.设![]() ,集合A是奇数集,集合B是偶数集.若命题p:
,集合A是奇数集,集合B是偶数集.若命题p:![]() ,则
,则
(A)![]() p:
p:![]() (B)
(B)![]() p:
p:![]()
(C)![]() p:
p:![]() (D)
(D)![]() p:
p:![]()
3.已知![]() 为实数,且
为实数,且![]() ,则“
,则“![]() ”是“
”是“![]() ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分也不必要条件
4.若![]() ,
,![]() ,则一定有
,则一定有
(A)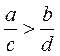 (B)
(B)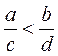 (C)
(C)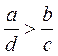 (D)
(D)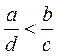
5.设![]() ,则使函数
,则使函数![]() 的定义域为
的定义域为![]() 且为奇函数的所有a的值为
且为奇函数的所有a的值为
(A)![]() (B)1,2,3 (C)1,3 (D)
(B)1,2,3 (C)1,3 (D)![]()
6.设a=![]() 6,
6,![]() ,
,![]() ,则
,则
(A)c>b>a (B)b>c>a (C)a>c>b (D)a>b>c
7.已知函数![]()
![]() ,若
,若![]() 存在唯一的零点
存在唯一的零点![]() ,且
,且![]() ,则a的取值范围为
,则a的取值范围为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
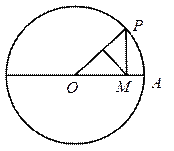 8.如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角
8.如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角![]() 的始边为射线
的始边为射线![]() ,终边为射线
,终边为射线![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,将点
,将点![]() 到直线
到直线![]() 的距离表示为
的距离表示为![]() 的函数
的函数![]() ,则
,则![]() =
=![]() 在[0,
在[0,![]() ]上的图象大致为
]上的图象大致为
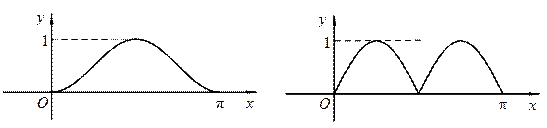
(A) (B)
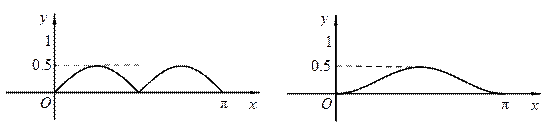
(C) (D)
9.设函数![]()
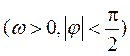 的最小正周期为
的最小正周期为![]() ,
,![]() ,则
,则
(A)![]() 在区间
在区间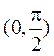 上单调递减
上单调递减
(B)![]() 在区间
在区间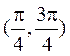 上单调递减
上单调递减
(C)![]() 在区间
在区间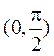 上单调递增
上单调递增
(D)![]() 在区间
在区间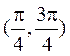 上单调递增
上单调递增
10.已知等比数列![]() 满足
满足![]() ,
,![]() ,则
,则![]()
![]()
(A)64 (B)81 (C)128 (D)24
11.设等差数列{an}的前n项和为Sn,Sm-1=![]() ,Sm=0,Sm+1=3,则m=
,Sm=0,Sm+1=3,则m=
(A)3 (B)4 (C)5 (D)6
12.不等式组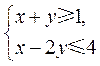 的解集记为D,现有下列四个命题:
的解集记为D,现有下列四个命题:
![]()
![]()
![]()
![]()
其中的真命题是
(A)p2,p3 (B)p1,p4 (C)p1,p2 (D)p1,p3
13.某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A原料1千克、B原