时间:2017-01-03 13:00:18
1、单选题 李工程师家里有4口人,母、妻、儿、本人。2013年,4人的年龄和为152岁,平均年龄正好比李工程师年龄小2岁,比妻子大2岁,若2007年时,妻子年龄正好是儿子的6倍,问哪一年时,母亲年龄正好是妻子年龄的2倍?_____
A: 2004年
B: 2006年
C: 2008年
D: 2010年
参考答案: B
本题解释:正确答案是B,全站数据:本题共被作答1次,正确率为0.00%,易错项为C解析在2013年,由总年龄152岁可知,4人平均年龄为152÷4=38岁,所以当年李工程师是40岁,妻子是36岁。则2007年妻子是30岁,所以儿子当年是5岁,即2013年儿子是11岁,得出母亲2013年是65岁。所以母亲和妻子的年龄差为6536=29岁,即妻子29岁是,母亲是她的2倍,即2006年。综合解析:首先由总和得到平均值;进而按照各年的条件关系,推出母亲和妻子的年龄差。解题的关键在于”年龄差不变”这个知识点,即若现在a比b多r岁,问多少年前a是b的2倍?解法的关键为:当a是b的2倍的时候,ab应该跟现在的年龄差r相等,所以ab=b=r,即b是r岁的时候,a是b的2倍。考点年龄问题笔记编辑笔记
2、单选题 如下图:已知直线P
A:y=kx+4与直线P
B:y=x+b相交于P(1,2),且分别与x轴、y轴交于点A、B。则四边形OAPB的面积是_____。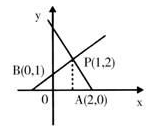 A: A
A: A
B: B
C: C
D: D
参考答案: C
本题解释:正确答案是C解析已知P
A:y=kx+4与直线P
B:y=x+b相交于P(1,2)。则k+4=2,1+b=2,解得k=-2,b=1,故P
A:y=-2x+4,P
B:y=x+1。PB与x轴交点为(-1,0),则底边长为2-(-1)=3。故有3×2÷2-1×1÷2=2.5,故正确答案为C。考点几何问题
3、单选题 ABCD四人去羽毛球馆打球,A每隔5天去一次,B每隔11天去一次,C每隔17天去一次,D每隔29天去一次,5月18日,四个人恰好在羽毛球馆相遇,则下一次相遇时间为?()
A: 9月18日
B: 10月14日
C: 11月14日
D: 12月18日
参考答案: C
本题解释:正确答案是C考点周期问题解析A、B、C、D四人的周期分别为6、12、18、30,因此周期的最小公倍数为180。从5月18日向后数180天,180天约为6个月,因此该时间必然落在11月,故正确答案为C。
4、单选题 “红星”啤酒开展”7个空瓶换1瓶啤酒”的优惠促销活动。现在已知张先生在活动促销期间共喝掉347瓶”红星”啤酒,问张先生最少用钱买了多少瓶啤酒?_____
A: 296瓶
B: 298瓶
C: 300瓶
D: 302瓶
参考答案: B
本题解释:正确答案是B考点计数模型问题解析7个空瓶换1瓶啤酒可表示为:7空瓶=1空瓶+1啤酒,可推知:6空瓶=1啤酒,假设最少要买x瓶,则有:x+[x/6]=347,将各选项代入知选项B中的298使得上述方程成立,故选择B选项。备注:此处的[x/6]表示取x/6的整数部分。标签直接代入
5、单选题 甲、乙、丙三个工程队的效率比为6:5:4,现将A、B两项工作量相同的工程交给这三个工程队,甲队负责A工程,乙队负责B工程,丙队参与A工程若干天后转而参与B工程。两项工程同时开工,耗时16天同时结束,问丙队在A工程中参与施工多少天?_____
A: 6
B: 7
C: 8
D: 9
参考答案: A
本题解释:正确答案是A考点工程问题解析解析1:根据题目给出的效率比,直接赋值三个工程队的效率分别为6、5、4,并假设丙队参与A工程Y天,则根据题意可得6×16+4Y=5×16+4(16-Y),解得Y=6。故正确答案为A。解析2:根据题目中的效率比,直接赋值三个工程队的效率分别为6、5、4,将两工程合在一起看整体,则三个工程队一天的工作量为6+5+4=15,则16天的总工作量为15×16=240,于是A工程的工作量为120,其中甲完成了6×16=96,则丙需要参与(120-96)÷4=6天。故正确答案为A。秒杀技秒杀1:将效率比看做份数,甲比乙每天多1份,16天则多16份,而丙一天完成4份,因此完成这16份需要4天,也即丙参与A工程比参与B工程少4天,于是参与A工程的天数为(16-4)÷2=6天。故正确答案为A。秒杀2:由题意甲效率高于乙效率,因此丙必然在甲中参与天数少于16天的一半,也即答案只在A、B中选择,这两个选项中,优先考虑代入A选项验证,符合条件,故正确答案为A。标签直接代入赋值思想