时间:2021-04-05 05:11:26
1、单选题 某班学生不到50人,在一次考试中,有1/7人得优,1/3人得良,1/2人及格,其余的均不及格,那么不及格的人数是_____。
A: 1
B: 2
C: 3
D: 4
参考答案: A
本题解释:正确答案是A考点倍数约数问题解析通过题干可知,该班级人数应为7、3、2的公倍数,又因为不能超过50人,所以该班人数为7×3×2=42人。那么不及格的人数为42-6-14-21=1。故正确答案为A。标签数字特性
2、单选题 射箭运动员进行训练,10支箭共打了93环,且每支箭的环数都不低8环。问命中10环的箭数最多能比命中9环的多几支?_____
A: 2
B: 3
C: 4
D: 5
参考答案: D
本题解释:正确答案是D,解析解析1:由题可知,”每支箭的环数都不低于8环”,所以环数只能取8、9、10环。假设10支箭都打了8环,则最低要打80环,而实际打的93环则是由于有9环和10环的贡献。与80环相比,每一个9环相当于多1环,每一个10环相当于多2环,所以设10环的有a支,9环的b支,则得到方程2a+b=93-80。这时,利用代入法,从”最多”的选项开始代入,a-b=5,解得a=6,b=1,即10环的是6支,9环是1支,8环是3支,可以成立。故正确答案为D。解析2:从另一个极端出发,如果每支箭的环数都打中10环,应该是100环,而实际为93环,少了7环。现在要求中10环的箭数”最多”能比命中9环的多几支,即要求10环尽量多,同时9环尽量少。所以少的7环尽可能由8环的箭产生,但是由于每支8环只能差2的整数倍,所以最多差6环,还需要有一支9环的。所以10环6支,9环1支,8环3支可以让差距最大。故正确答案为D。速解如果列方程,属于不定方程,未知数的个数多于方程个数,需要靠代入法解决。而题目真正的考点在于”最多”这个词的理解,即10环尽量多,9环尽量少,在这个前提下分析题目,才能得到最简的方式。考点计数模型问题笔记编辑笔记
3、单选题 一个自然数,被7除余2,被8除余3,被9除余1,1000以内一共有多少个这样的自然数?_____
A: 5
B: 2
C: 3
D: 4
参考答案: B
本题解释:参考答案:B
题目详解:7、8的最小公倍数为56,根据"差同减差,公倍数做周期"可知:所有满足条件的数可表示为56n-5,也就是除以56余5;要让所有56n-5中满足被9除余1:最小数是n=3时: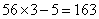
4、单选题 现在有64个乒乓球,18个乒乓球盒,每个盒子里最多可以放6个乒乓球,最少要放1个乒乓球,至少有几个乒乓球盒子里的乒乓球数目相同?_____
A: 4
B: 5
C: 8
D: 10
参考答案: A
本题解释:参考答案:A
题目详解:假设第一只盒子装1个乒乓球,第二只盒子装2个乒乓球,第三只盒子装3个乒乓球,第四只盒子装4个乒乓球,第五只盒子装5个乒乓球,第六只盒子装6个乒乓球。由于最多只能装6个乒乓球,所以第七到第十二也只能是这种情况,第十三到第十八也相同。第一到第六个盒子共装了21个乒乓球,第一到第十八个盒子装了21×3=63个乒乓球,此时有三个盒子装的乒乓球数量一样多。所以如果将第64个乒乓球算上,则有四个盒子装的乒乓球数量一样多。考查点:数量关系>数学运算>抽屉原理问题>抽屉原理1
5、单选题 若干个相同的立方体摆在一起,前、后、左、右的视图都是 A: 4
A: 4
B: 6
C: 8
D: 10
参考答案: A
本题解释:正确答案是A考点几何问题解析从最少的情况考虑,如下图所示即可实现。右图为俯视情况,其中阴影表示放置有立方体的位。