时间:2017-03-05 16:29:00
1、计算题 如图所示，在坐标xoy平面内存在B=2.0T的匀强磁场，OA与OCA为置于竖直平面内的光滑金属导轨，其中OCA满足曲线方程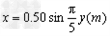
，C为导轨的最右端，导轨OA与OCA相交处的O点和A点分别接有体积可忽略的定值电阻R1和R2，其R1=4.0Ω、R2=12.0Ω。现有一足够长、质量m=0.10 kg的金属棒MN在竖直向上的外力F作用下，以v=3.0m/s的速度向上匀速运动，设棒与两导轨接触良好，除电阻R1、R2外其余电阻不计，g取10m/s2，求：
（1）金属棒MN在导轨上运动时感应电流的最大值；
（2）外力F的最大值；
（3）金属棒MN滑过导轨OC段，整个回路产生的热量。
参考答案：
解：（1）金属棒MN沿导轨竖直向上运动，进入磁场中切割磁感线产生感应电动势。当金属棒MN匀速运动到C点时，电路中感应电动势最大，产生的感应电流最大
金属棒MN接入电路的有效长度为导轨OCA形状满足的曲线方程中的x值。因此接入电路的金属棒的有效长度为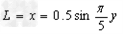
，Lm=xm=0.5m
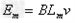，Em=3.0V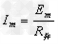
且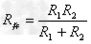
?
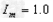A
（2）金属棒MN匀速运动中受重力mg、安培力F安、外力F外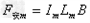
，
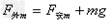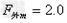N
，
N
（3）金属棒MN在运动过程中，产生的感应电动势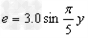
?
有效值为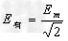
金属棒MN滑过导轨OC段的时间为t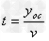
，
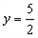m，
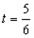s?
滑过OC段产生的热量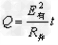
，
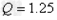J
本题解析：
本题难度：困难
2、选择题 吉他以其独特的魅力吸引了众多音乐爱好者，电吉他与普通吉他不同的地方是它的每一根琴弦下面安装了一种叫“拾音器”的装置，能将琴弦的振动转化为电信号，电信号经扩音器放大，再经过扬声器就能播出优美音乐．如图所示是拾音器的结构示意图，多匝线圈置于永久磁铁与钢制的琴弦之间，当琴弦在线圈上振动时，线圈中就会产生感应电流．下列说法正确的是（ ）
A．电吉他可以使用尼龙线做琴弦
B．琴弦振动时，线圈中产生感应电流是恒定的
C．电吉他是根据电磁感应原理工作的
D．琴弦振动时，线圈中产生感应电流是大小和方向都变化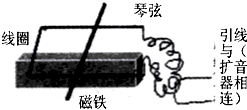
参考答案：A、电吉他不可以使用尼龙线做琴弦．若是尼龙线则不能构成回路，故A错误；
B、琴弦振动时，线圈中产生感应电流是变化的，若是恒定，则声音全是一种调，更何况也不可是恒定电流的．故B错误；
C、电吉他是属于磁生电，是根据电磁感应原理工作的．故C正确；
D、琴弦振动时，线圈中产生感应电流大小和方向均在变化的．故正确；
故选：CD．
本题解析：
本题难度：简单
3、选择题 水平放置的U形光滑金属导轨上放置一金属棒ab，甲图中的矩形区域内存在一有界匀强磁场，规定垂直纸面向里为磁场正方向。现使该磁场按乙图所示的规律变化，则下列判断正确的是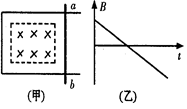 
A．ab棒中将产生从a到b方向的电流，同时ab棒将在导轨上向右滑动
B．ab棒中将产生从b到a方向的电流，同时ab棒将在导轨上向左滑动
C．ab棒中将产生先从a到b方向后从b到a方向的电流，ab棒将在导轨上先向右后向左滑动
D．ab棒中将产生从a到b方向的电流，ab棒不会在导轨上滑动
参考答案：D
本题解析：穿过线圈的磁通量先正向减小，由楞次定律可判断此时电流为顺时针，后磁通量负方向增大，感应电流的磁场垂直纸面向外，由右手定则可知电流方向为顺时针，但导体棒ab处没有磁场，所以ab不受安培力作用，D对；
本题难度：简单
4、简答题 在光滑的水平面上存在着两个磁感应强度大小相等，方向相反的匀强磁场区域，其宽度均为l，如图所示．一个质量为m、边长为l的正方形线框，在水平恒力作用下，从静止开始运动l，速度达到v0，进人左边磁场时恰好作匀速运动．求：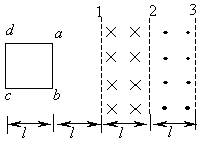
(1)当ab边刚越过中界线2时，线框的加速度．
(2)当ab边刚越过中界线2和边界线3的中间位置时，线框又恰好做匀速运动，求线框从开始进人边界线1到ab边到达界线2、3中间位置的过程中，共产生多少热量．
?
参考答案：（1）3v02/2l?（2）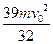
本题解析：
(1)从开始运动到速度达到v0的过程中，加速度大小a1=v02/2l．
在左边磁场中运动时受力平衡，即安培力等于拉力F，即F=BIl．
当ab边刚越过中界线2时，两边产生的感应电动势相加而产生感应电流，其大小为
I’=2I，每边受到的安培力都是原来的2倍．这时两边受的安培力都向左，与拉力F反向，这时的加速度大小为a=3a1=3v02/2l．
(2)当ab边刚越过中界线2和边界线3的中间位置时，线框又恰好受力平衡，设这时的速度为v’，则4B2l2v’/R=F，这说明v’=v0/4．
根据功能关系，线框从开始进人边界线1到ab边到达界线2、3中间位置的过程中产生的热量等于拉力F做的功与动能减少量之和，
即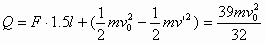
．
本题难度：一般
5、计算题 如图所示，两平行的光滑金属导轨安装在一光滑绝缘斜面上，导轨间距为l、足够长且电阻忽略不计，导轨平面的倾角为α，条形匀强磁场的宽度为d，磁感应强度大小为B、方向与导轨平面垂直。长度为2d的绝缘杆将导体棒和正方形的单匝线框连接在一起组成“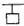
”型装置，总质量为m，置于导轨上。导体棒中通以大小恒为I的电流（由外接恒流源产生，图中未画出）线。框的边长为d（d< l），电阻为R，下边与磁场区域上边界重合。将装置由静止释放，导体棒恰好运动到磁场区域下边界处返回，导体棒在整个运动过程中始终与导轨垂直。重力加速度为g。求：
（1）装置从释放到开始返回的过程中，线框中产生的焦耳热Q；
（2）线框第一次穿越磁场区域所需的时间t1；
（3）经过足够长时间后，线框上边与磁场区域下边界的最大距离Xm。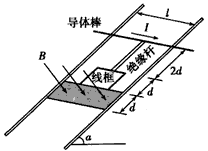
参考答案：解：（1）设装置由静止释放到导体棒运动到磁场下边界的过程中，作用在线框上的安培力做功为W
由动能定理mgsinα·4d+W－BIld=0
且Q= -W
解得Q=4mgdsinα－BIld
（2）设线框刚离开磁场下边界时的速度为v1，则接着向下运动2d
由动能定理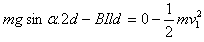
装置在磁场中运动时受到的合力F=mgsinα－F"
感应电动势ε=Bdv
感应电流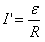
安培力F"=Bl"d
由牛顿第二定律，在t到t+△t时间内，有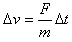
则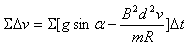
有v1=gt1sin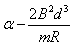
解得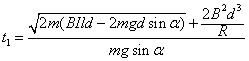
（3）经过足够长时间后，线框在磁场下边界与最大距离Xm之间往复运动
由动能定理mgsinα·Xm－BIl（Xm－d）=0
解得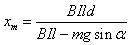
本题解析：
本题难度：困难